Представленные в предыдущем пункте канонические разложения могут
служить основой для получения новых разложений. Так, положив 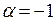 и
и
в последнем разложении, мы получим формулы суммы бесконечной
геометрической прогрессии со знаменателем 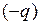 :
: 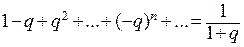 . Заменив в этой формуле
. Заменив в этой формуле 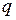 на
на 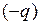 , получим:
, получим:
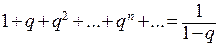 .
.
Заменим в последней формуле 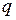 на
на 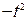 , мы получим разложение
, мы получим разложение
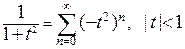 . Последний ряд имеет радиус сходимости, равный 1. Вспомним, что внутри интервала сходимости ряды можно интегрировать
. Последний ряд имеет радиус сходимости, равный 1. Вспомним, что внутри интервала сходимости ряды можно интегрировать
почленно и проинтегрируем обе части последнего равенства по 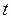 от 0 до
от 0 до
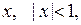 тогда получим разложение:
тогда получим разложение: 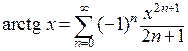 .
.
Выше, там, где мы говорили о функциях, не имеющих первообразной,
выраженной через элементарные функции, был приведен пример функции 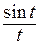 . Благодаря простому разложению этой функции в ряд Тейлора, ее можно проинтегрировать по отрезку
. Благодаря простому разложению этой функции в ряд Тейлора, ее можно проинтегрировать по отрезку 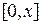 и получить новую функцию, называемую интегральным синусом:
и получить новую функцию, называемую интегральным синусом: 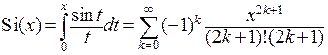 .
.
 2014-02-18
2014-02-18 1011
1011







