2014-02-18
534
Дисперсия альтернативного признака.
Среди множества варьирующих признаков, изучаемых статистикой, существуют признаки, которыми обладают одни единицы совокупности и не обладают другие. Эти признаки называются альтернативными. Альтернативный признак принимает всего два значения – 0 и 1 с весами соответственно p и q. Поэтому среднее значение альтернативного признака равно р. А дисперсия альтернативного признака равна pq. Дисперсия альтернативного признака равна произведению доли признака, обладающего характеристикой на долю признака, не обладающего характеристикой. Предельное значение дисперсии для альтернативного признака равно 0,25 при р=0,5.
Дисперсия альтернативного признака широко применяется в выборочном обследовании.
Изменения частот в вариационных рядах изменяются закономерно в связи с изменением варьирующего признака. Такие закономерности называются закономерностями распределения.
Основная задача анализа вариационных рядов заключается в выявлении подлинной закономерности распределения путем исключения влияния второстепенных, случайных для данного распределения факторов.
Если увеличить объем совокупности и уменьшить интервал в группах, то графическое изображение приближается к некоторой плавной кривой, которая называется кривой распределения.
Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.
Теоретическая кривая распределения (distribution curve) – кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него факторов.
Выяснение общего характера распределения предполагает оценку его однородности, а также расчет показателей асимметрии и эксцесса.
При сравнительном изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии (skewness):
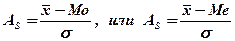
Его величина может быть положительной (для правосторонней асимметрии) и отрицательной (для левосторонней асимметрии).
Если асимметрия >= 0,5 (независимо от знака), то смещение считается значительным. Если асимметрия <= 0,25, то она считается незначительной.
Наличие асимметрии в генеральной совокупности проверяется с помощью определения оценки существенности на основе средней квадратической ошибки (standard error of skewness):
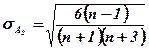
В случае, если t-критерий Стьюдента (t-parameter)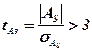 
, асимметрия считается существенной и распределение признака в генеральной совокупности несимметрично и неслучайно, а закономерно.
Для симметричных распределений может быть рассчитан показатель эксцесса (kurtosis), который показывает, насколько резкий скачок имеет изучаемое явление. Показатель эксцесса определяется на основе центрального момента четвертого порядка по формуле:
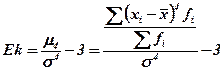
Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным. Среднеквадратическая ошибка эксцесса (standard error of kurtosis) показывает, насколько существенен скачок в явлении и рассчитывается по формуле:
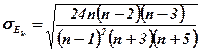
В случае, если t-критерий Стьюдента (t-parameter)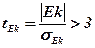 
, то эксцесс считается существенным и распределение признака в генеральной совокупности характеризуется заметными скачками и является неслучайным, а закономерным.
