2014-02-18
354
Моменты распределения.
Для описания особенностей распределения используют такую характеристику, как момент. Момент k-го порядка это средний размер k-ой степени отклонений всех значений признака x от какой-либо величины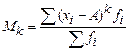 
Моменты характеризуются видом и порядком. В зависимости от величины A рассматривают следующие виды моментов:
- начальные, при А=0
- центральные, при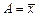 
- условные, при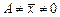 
Порядок момента характеризуется показателем степени отклонения. Различают моменты первого, второго, третьего, четвертого порядка.
Формулы расчета моментов представлены в таблице 13.
Таблица 13
Формулы расчета моментов
| Поря- док мо-мен-тов | Виды моментов | ||
| начальные | центральные | условные | |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
|
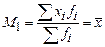
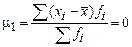
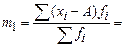
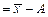
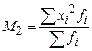
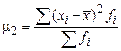
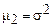
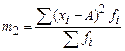
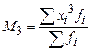
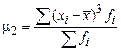
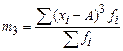
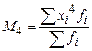
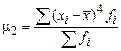
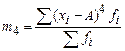
При сравнении эмпирической и теоретической кривых распределения обращают внимание на показатели асимметрии распределения и на эксцесс – крутизну распределения по сравнению с нормальной.
Асимметрию можно измерить с помощью коэффициента асимметрии Пирсона, который рассчитывается по формуле: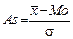 
. Если 
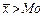, то говорят о правосторонней асимметрии, если 
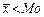, то асимметрия левосторонняя.
|
|
|
Эксцесс – крутизна распределения по сравнению с нормальной вычисляется с помощью нормированного момента 4 порядка по формуле: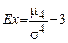 
. При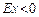 
говорят о низковершинности распределения, а при 
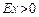- о высоковершинностираспределения.
