Таким образом, свободной частице в квантовой механике сопоставляется плоская монохроматическая волна де Бройля

13.2 Решение стационарного уравнения Шредингера для частицы
в бесконечно глубокой прямоугольной потенциальной яме

Рассмотрим движение частицы вдоль направления х, при этом движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U в этом случае равна (рис.13.1):

U = 0 при 0 £ x £ l,

U = ∞ при x < 0 и x > l.

Уравнение Шредингера в этом случае имеет вид:

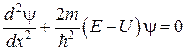. (13.3)

Вероятность обнаружить частицу за пределами ямы равна нулю, так как частица не может обладать бесконечно большой энергией. Из условия непрерывности волновой функции следует, что 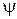должна быть равна нулю и на границах ямы, т. е.

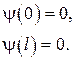(13.4)

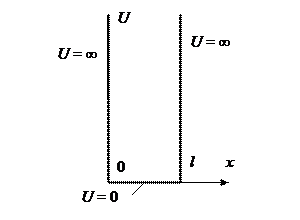
Рис. 13.1

В области, где y не равна тождественна нулю, уравнение (13.3) принимает вид:

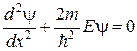. (13.5)

Обозначим 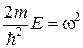, тогда (13.5) примет вид

.

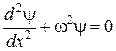Решение такого уравнения, как известно, имеет вид:

y(x) = A sin(w x + a).

Найдем w и a, используя граничные условия (13.4) Из условия y(0) = 0 получаем:

y(0) = A sin a = 0,

откуда следует, что a = 0. Из условия, что y(l) = A sin w l = 0 имеем:

w l = ±p n, (n = 1, 2, 3, …). (13.6)

Из соотношения (13.6) вытекает, что решение уравнения (13.5) будут иметь физический смысл не при всех значениях энергии Е, а только при значениях, удовлетворяющих условию:

(n = 1, 2, 3, …)

откуда:

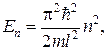(n = 1, 2, 3, …). (13.7)

Соотношение (13.7) указывает на то, что другие значения энергии частицы чем E_n невозможны: вероятность обнаружить внутри потенциальной ямы частицу с энергией, отличной от E_n , равна нулю. Физические величины, которые могут принимать лишь определенные дискретные значения, называются квантованными.