Показатели размера и интенсивности вариации

Для измерения размера и интенсивности вариации значений признака используют абсолютные и относительные показатели.

К абсолютным показателям вариации относят: размах вариации R, среднее линейное отклонение 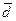, дисперсию 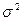, среднее квадратическое отклонение (табл. 18).

Таблица 18

Абсолютные показатели вариации

Название показателя	Формула расчета
при использовании индивидуальных данных	при использовании сгруппированных данных
1. Размах вариации 2. Среднее линейное отклонение 3. Дисперсия 4. Среднее квадратическое отклонение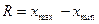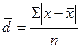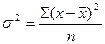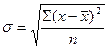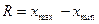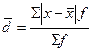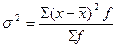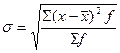

Размах вариации является простейшим и самым приблизительным показателем. В его исчислении участвуют лишь два крайних значения признака (максимальное и минимальное), поэтому он не отражает закономерностей вариации всей совокупности.

В нашем примере размах вариации сменной выработки деталей составляет: в первой бригаде – R₁ = 10 шт. (то есть 105 – 95); во второй бригаде – R₂ = 50 шт. (то есть 125 – 75), что в 5 раз больше. Это свидетельствует о том, что при численном равенстве средняя выработка первой бригады более «устойчива». Размах вариации может служить базой расчета возможных резервов роста выработки. Таких резервов больше у второй бригады, поскольку в случая достижения всеми рабочими максимальной для этой бригады выработки деталей, ею может быть изготовлено 375 шт., то есть (3 х 125), а в первой – только 315 шт., то есть (3 х 105).

Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику. Простейший показатель такого типа – среднее линейное отклонение.

Среднее линейное отклонение учитывает все отклонения индивидуальных значений признака от средней величины, но без учета знака (это связано с одним из свойств средней арифметической: Σ (х - 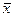) = 0). Этот показатель отражает среднее отклонение значений изучаемого признака от средней величины, легко интерпретируется и рассчитывается, но его нельзя поставить в соответствии с каким-либо вероятностным законом, в том числе и с нормальным распределением.

Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных).

Формулы дисперсий можно преобразовать, учитывая, что

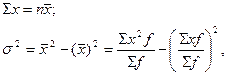
то есть дисперсия равна разности средней из квадратов вариантов и квадрата их средней.

Дисперсия не имеет единиц измерения.

Среднее квадратическое отклонение есть корень квадратный из дисперсии. В реальных совокупностях σ всегда больше 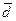. Соотношение 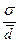зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить показателем неоднородности совокупности (чем выше это соотношение, тем больше степень неоднородности). Для нормального закона распределения σ ≈1,25.

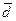Абсолютные показатели вариации отражают с различной степенью точности размеры вариации в изучаемой совокупности, но не позволяют:

1) судить об интенсивности вариации значений признака;

2) сравнивать размеры вариации в различных совокупностях.

Для этого используются относительные показатели вариации. Они рассчитываются как отношение абсолютных показателей вариации к средней арифметической величине признака. К таким показателям относят:

1) относительный размах вариации -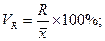

2) относительное среднее линейное отклонение -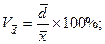

3) коэффициент вариации -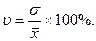

Оценка степени интенсивности вариации возможна только в отношении каждого отдельного признака и совокупности определенного состава. Такая оценка заключается в сравнении относительного показателя вариации (чаще всего коэффициента вариации) с некоторой обычной величиной, принимаемой за норматив.

Если коэффициент вариации составляет не менее 33,3 %, исследуемая совокупность считается весьма неоднородной и для проведения дальнейшего анализа должна быть разгруппирована.

Отношение размаха вариации к средней арифметической в процентах называется коэффициентом осцилляции:

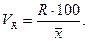
В нормальном ряду распределения между 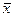, D, σ, R существуют определенные соотношения.

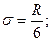следовательно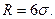

Зная 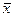и σ, можно представить размах вариации как R =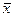± 3σ.

При достаточно большом объеме совокупности между σ и D существует соотношение σ = 1,25 D.