Лекция 4. Аналитическая геометрия на плоскости
4.1. Простейшие задачи
4.2. Уравнение линии
4.3. Прямая линия на плоскости
4.4. Линии второго порядка
4.5. Полярная система координат
4.6. Параметрические уравнения линий
4.1. Простейшие задачи
Аналитическая геометрия – раздел математики, в котором изучаются геометрические объекты с помощью алгебраических методов.
Основным методом аналитической геометрии является метод координат.
Рассмотрим простейшие задачи.
1. Расстояние 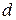 между двумя точками
между двумя точками 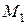
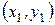 и
и 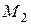
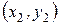 определяется как длина вектора
определяется как длина вектора 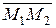 по формуле
по формуле 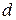 =
=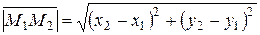 .
.
2.  Координаты точки
Координаты точки 
 , делящей отрезок
, делящей отрезок  , где
, где 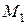
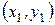 ,
, 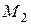
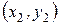 , в данном отношении
, в данном отношении 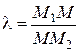
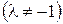 определяются формулами
определяются формулами 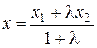 ,
, 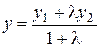 .
.
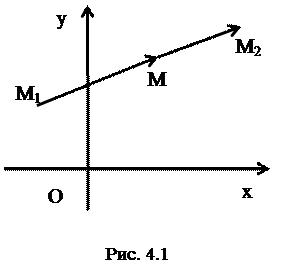
Рассмотрим вывод этих формул. Очевидно, что 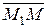 =
=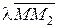 (рис.4.1).
(рис.4.1). 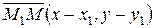 ,
, 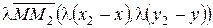 .
.
Отсюда 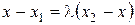 ,
, 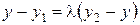 .
.
Из последних соотношений получаем, что 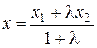 ,
, 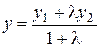 .
.
 Если
Если 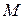 - середина отрезка
- середина отрезка  , то
, то  =1 и
=1 и 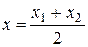 ,
, 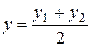 .
.
Пример. Вычислить длины медиан треугольника с вершинами 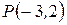 ,
, 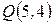 ,
, 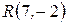 .
.
Решение. Пусть 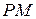 ,
, 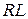 ,
, 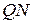 - медианы треугольника
- медианы треугольника 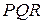 ,
, 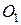 - точка их пересечения (рис.4.2).
- точка их пересечения (рис.4.2).
Так как 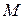 - середина отрезка
- середина отрезка 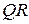 , то
, то 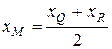 ,
, 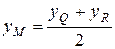 .
.
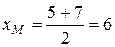 ,
, 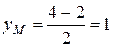 .
.
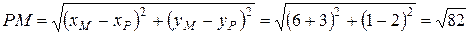 .
.
Аналогично находим 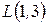 ,
, 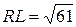 ,
, 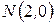 ,
, 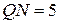 .
.
4.2. Уравнение линии
Линия на плоскости задается как некоторое геометрическое место точек, обладающих некоторым свойством, исключительно им присущих.
Определение.Уравнением линии на плоскости называется уравнение относительно переменных 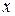 и
и 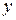 , которому удовлетворяют координаты любой точки данной линии и только они.
, которому удовлетворяют координаты любой точки данной линии и только они.
В общем виде уравнение линии на плоскости в прямоугольных декартовых координатах записывается так: 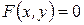 .
.
Из определения уравнения линии вытекает, что если при подстановке координат точки в данное уравнение получаем тождество, то точка лежит на соответствующей линии; если тождество не получается, то точка не лежит на этой линии.
Чтобы составить уравнение линии, как некоторого геометрического места точек, необходимо:
1) взять произвольную точку линии с текущими координатами 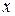 ,
, 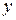 ;
;
2) записать общее свойство точек данного геометрического места в виде равенства;
3) выразить входящие в это равенство величины с помощью координат.
Точки пересечения двух линий 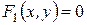 и
и 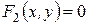 находят из системы уравнений
находят из системы уравнений
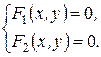
Если система имеет действительные решения, то линии пересекаются. Если же действительных решений нет, то линии общих точек не имеют.
4.3. Прямая линия на плоскости
4.3.1. Нормальный вектор прямой. Уравнение прямой,
проходящей через данную точку перпендикулярно заданному вектору
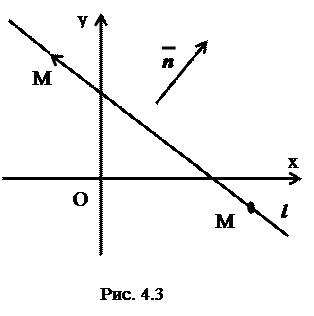
Выведем уравнение прямой линии в декартовой прямоугольной системе. Рассмотрим на плоскости 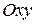 произвольную прямую
произвольную прямую 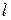 (рис.4.3).
(рис.4.3).
Пусть 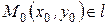 ,
, 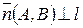 .
.
Вектор 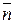 называется нормальным вектором прямой. Точка
называется нормальным вектором прямой. Точка 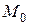 и вектор
и вектор 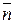 вполне определяют положение прямой на плоскости
вполне определяют положение прямой на плоскости 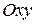 .
.
Пусть 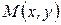 - текущая точка прямой
- текущая точка прямой  .
.
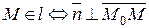
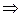
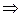
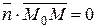
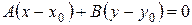 . (1)
. (1)
Уравнение (1) есть уравнение прямой, проходящей через данную точку перпендикулярно заданному векто ру.
4.3.2. Общее уравнение прямой
Уравнение (1) есть уравнение первой степени относительно текущих координат 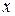 и
и 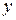 . Покажем, что и, обратно, любое уравнение первой степени
. Покажем, что и, обратно, любое уравнение первой степени
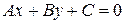 (2)
(2)
относительно координат 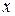 и
и 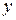 есть уравнение некоторой прямой, лежащей в плоскости
есть уравнение некоторой прямой, лежащей в плоскости 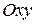 .
.
Пусть в уравнении (2) 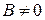 . Тогда это уравнение равносильно уравнению
. Тогда это уравнение равносильно уравнению
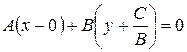 (3).
(3).
Но уравнение (3) есть уравнение прямой, проходящей через точку 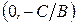 перпендикулярно вектору
перпендикулярно вектору 
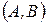 . Следовательно, и (2) является уравнением этой прямой. Оно называется общим уравнением прямой.
. Следовательно, и (2) является уравнением этой прямой. Оно называется общим уравнением прямой.
Исследуем уравнение (2).
1. Если 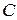 =0, то уравнение (2) принимает вид
=0, то уравнение (2) принимает вид 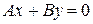 и определяет прямую, проходящую через начало координат.
и определяет прямую, проходящую через начало координат.
2. Если 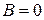
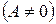 , то уравнение (2) принимает вид
, то уравнение (2) принимает вид 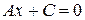
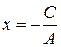 и определяет прямую, параллельную оси
и определяет прямую, параллельную оси 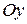 . При
. При 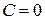 эта прямая совпадает с осью
эта прямая совпадает с осью 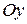 .
.
2. Если 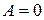
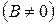 , то уравнение (2) принимает вид
, то уравнение (2) принимает вид 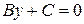
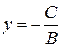 и определяет прямую, параллельную оси
и определяет прямую, параллельную оси 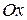 . При
. При 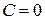 эта прямая совпадает с осью
эта прямая совпадает с осью 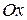 .
.
4.3.3. Уравнение прямой с угловым коэффициентом
Пусть в уравнении (2) 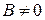 . Тогда
. Тогда 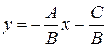 . Обозначая
. Обозначая 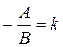 ,
, 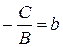 , получаем уравнение
, получаем уравнение 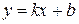 - уравнение прямой с угловым коэффициентом.
- уравнение прямой с угловым коэффициентом.
4.3.4. Уравнение прямой, проходящей через данную точку
 Из уравнения (1) при
Из уравнения (1) при 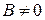 (
(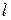
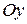 ) следует
) следует 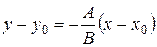 .
.
Обозначая 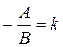 , получаем уравнение
, получаем уравнение 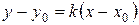 - уравнение прямой, проходящей через данную точку.
- уравнение прямой, проходящей через данную точку.
4.3.5. Уравнение прямой, проходящей через две точки.
Уравнение прямой в отрезках
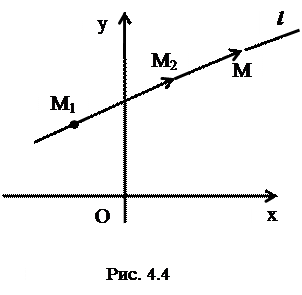 Пусть
Пусть 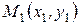 ,
, 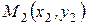
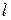 - фиксированные точки прямой
- фиксированные точки прямой 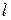 ,
, 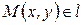 - текущая точка прямой
- текущая точка прямой 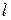 (рис.4.4).
(рис.4.4). 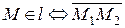 .||
.|| 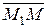 ,
,
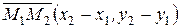 ,
,
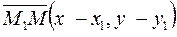 .
.
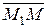 ||
|| 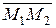
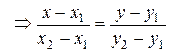 - уравнение прямой, проходящей через две точки.
- уравнение прямой, проходящей через две точки.
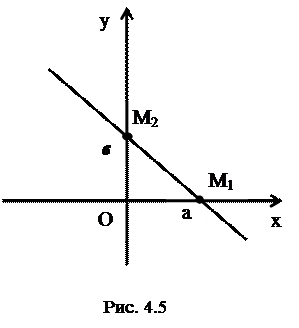 Пусть прямая
Пусть прямая 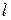 отсекает на осях координат отрезки длиной
отсекает на осях координат отрезки длиной 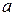 и
и 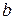 (рис.4.5).
(рис.4.5). 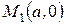 ,
, 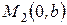
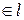 .
.
Отсюда, исходя из уравнения прямой, проходящей через две точки, получаем 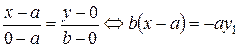 ,
,
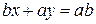
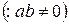
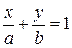 - уравнение прямой в отрезках.
- уравнение прямой в отрезках.
4.3.6. Каноническое уравнение прямой. Параметрические уравнения прямой
 Рассмотрим на плоскости
Рассмотрим на плоскости 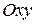 произвольную прямую
произвольную прямую 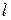 . Ее положение вполне определяется заданием точки
. Ее положение вполне определяется заданием точки 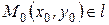 и вектора
и вектора 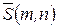 ||
|| 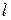 . Вектор
. Вектор 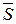 при этом называется направляющим вектором прямой
при этом называется направляющим вектором прямой 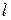 (рис. 4.6).
(рис. 4.6). 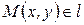 - текущая точка прямой.
- текущая точка прямой.
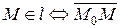 ||
|| 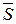
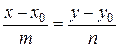 -
-
каноническое уравнение прямой.
Обозначим 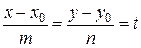 , где
, где 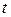 - параметр.
- параметр.
Тогда 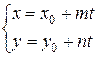 - параметрические уравнения прямой.
- параметрические уравнения прямой.
4.3.7. Расстояние от точки до прямой
Пусть на плоскости  заданы прямая
заданы прямая 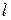 :
: 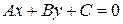 и точка
и точка 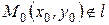 .
.
Тогда расстояние от точки 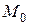 до прямой
до прямой 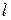 находится по формуле
находится по формуле
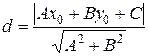 .
.
Пример 1. Треугольник задан своими вершинами 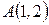 ,
, 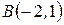 и
и 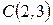 . Найти длину его высоты, опущенной из вершины
. Найти длину его высоты, опущенной из вершины 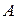 .
.
Решение. Найдем уравнение прямой, проходящей через две точки 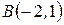 и
и 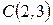 :
:
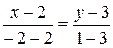 или
или 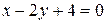 . Тогда
. Тогда 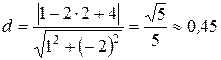 .
.
4.3.8. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
Пусть две пересекающиеся в точке 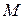 прямые
прямые 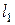 и
и 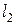 определяются соответственно уравнениями
определяются соответственно уравнениями
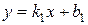 и
и 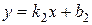 (рис.4.7).
(рис.4.7).
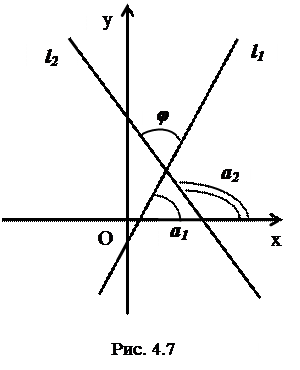
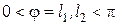
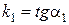 ,
, 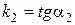 .
.
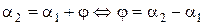 .
.
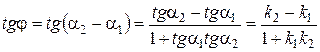
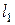 ||
||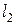
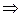
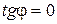
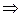
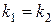 .
.
Справедливо и обратное условие.
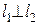
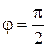
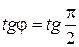 не существует,
не существует, 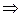 1+
1+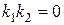
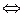
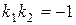 .
.
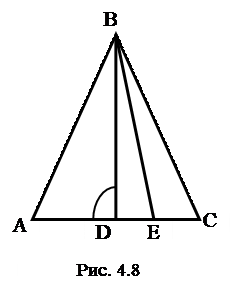
Пример 2. В треугольнике с вершинами 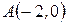 ,
, 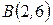 и
и 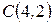 проведены высота
проведены высота 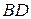 и медиана
и медиана 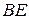 . Написать уравнения стороны
. Написать уравнения стороны 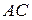 , медианы
, медианы 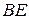 и высоты
и высоты 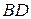 (рис.4.8).
(рис.4.8).
 Решение.
Решение.
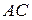 :
: 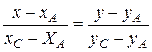 .
. 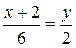 .
.
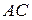 :
: 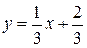 .
.  - середина отрезка
- середина отрезка 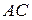 ,
, 
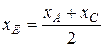 ,
, 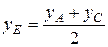 .
.
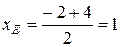 ,
, 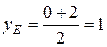 ,
, 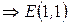 .
.
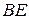 :
: 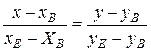 .
. 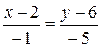 .
. 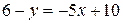 .
.
 2014-02-09
2014-02-09 1577
1577