:.
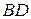 :
: 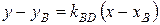
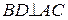


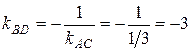 ,
,
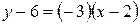 ,
,

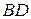 :
: 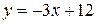 .
.
4.4. Линии второго порядка
Прямая – это алгебраическая линия первого порядка. Что касается алгебраических линий 2-го порядка, то к ним относятся окружность, эллипс, парабола и гипербола (не считая случаев их вырождения).
Общий вид уравнения линии 2-го порядка 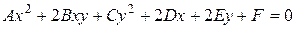 , где
, где 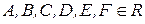 , при этом хотя бы один из коэффициентов отличен от нуля.
, при этом хотя бы один из коэффициентов отличен от нуля.
4.4.1. Окружность
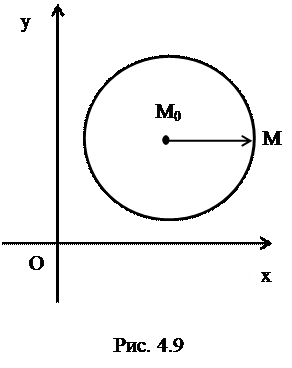
Определение 1. Окружность – это множество точек 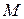 плоскости, равноотстоящих от данной точки
плоскости, равноотстоящих от данной точки 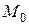 , называемой центром (рис.4.9).
, называемой центром (рис.4.9).
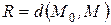 -
-
- радиус окружности. Составим урав-нение окружности в прямоугольных декартовых координатах.
Пусть 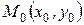 ,
, 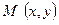 .
.
Тогда 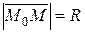


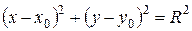 .
.
Если 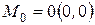 , то получаем каноническое уравнение окружности
, то получаем каноническое уравнение окружности 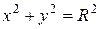 .
.
Пример 1. Определить координаты центра и радиус окружности
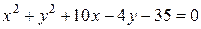 .
.
Решение. Выделим полные квадраты относительно переменных  и
и  :
:
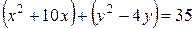

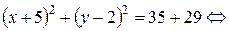
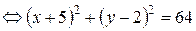 .
.
Следовательно, 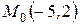 ,
, 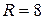 .
.
4.4.2. Эллипс
Определение 2. Эллипсом называется множество всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек (фокусов) той же плоскости есть величина постоянная (большая, чем расстояние между фокусами).
Обозначим фокусы буквами 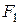 и
и 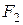 , расстояние между ними – через 2 с, т.е.
, расстояние между ними – через 2 с, т.е. 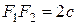 , и назовем фокусным расстоянием.
, и назовем фокусным расстоянием.
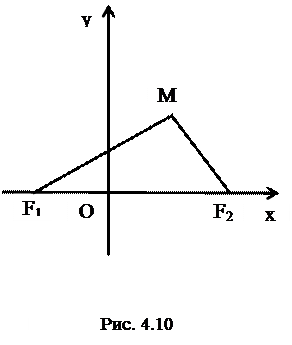 Постоянную величину, о которой идет речь в определении 2, обозначим через
Постоянную величину, о которой идет речь в определении 2, обозначим через 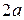 . Пусть
. Пусть 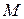 - произвольная точка эллипса, тогда по определению 2,
- произвольная точка эллипса, тогда по определению 2, 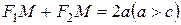 . Составим уравнение эллипса в прямоугольных декартовых координатах. Выберем ось
. Составим уравнение эллипса в прямоугольных декартовых координатах. Выберем ось 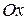 так, чтобы она проходила через фокусы (рис. 4.10) и имела положительное направление от
так, чтобы она проходила через фокусы (рис. 4.10) и имела положительное направление от 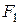 к
к 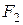 . Начало координат поместим в середине отрезка
. Начало координат поместим в середине отрезка 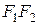 , тогда
, тогда 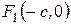 ,
, 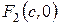 .
. 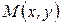 - текущая точка эллипса. Тогда из определения 2 получаем иррациональное уравнение
- текущая точка эллипса. Тогда из определения 2 получаем иррациональное уравнение
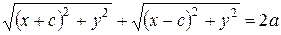

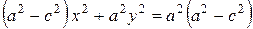 . Так как
. Так как 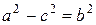 ,
, 
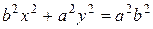
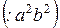

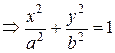 (1)
(1)
 – каноническое уравнение эллипса.
– каноническое уравнение эллипса.
Этому уравнению удовлетворяют координаты любой точки эллипса. Нетрудно убедиться в том, что справедливо обратное утверждение: если координаты точки  удовлетворяют уравнению (1), то точка
удовлетворяют уравнению (1), то точка  лежит на эллипсе. Из уравнения (1) следует, что
лежит на эллипсе. Из уравнения (1) следует, что 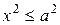 , т.е.
, т.е. 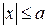
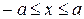 и
и 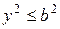
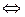
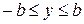 .
.
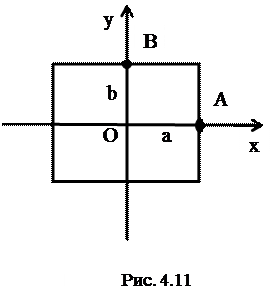
Последнее означает, что эллипс расположен целиком в прямоугольнике, основание которого равно 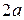 , а высота
, а высота 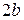 , центр находится в начале координат (рис. 4.11).
, центр находится в начале координат (рис. 4.11).
Так как в уравнение (1) 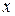 и
и 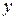 входят в четной степени, то эллипс симметричен относительно осей
входят в четной степени, то эллипс симметричен относительно осей 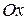 и
и  .
.
В силу этого достаточно исследовать его форму в первой четверти. Тогда из (1) получаем 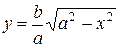 . Отсюда видно, что если
. Отсюда видно, что если 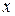 возрастает от 0 до
возрастает от 0 до 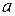 , то
, то 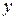 убывает от
убывает от 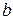 до 0;
до 0;
при 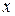 =0
=0 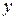 =
=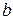 , получаем точку
, получаем точку 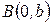 , при
, при 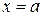
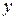 =0 – точку
=0 – точку 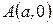 .
.
Соответствующая дуга эллипса, расположенная в первой четверти, изображена на рис. 4.12, (а), а весь эллипс – на рис. 4.12 (б).
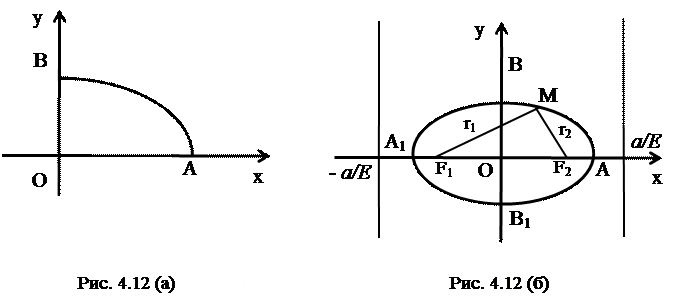
Точки пересечения эллипса с координатными осями называются вершинами эллипса (точки  ,
,  ,
, 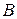 ,
, 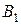 на рис. 4.12 (б)).
на рис. 4.12 (б)).
Оси симметрии эллипса (оси 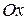 и
и 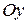 ) называются просто осями, точка пересечения осей – центром эллипса. Осями называются также отрезки
) называются просто осями, точка пересечения осей – центром эллипса. Осями называются также отрезки 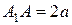 ,
, 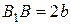 , полуосями – отрезки
, полуосями – отрезки  ,
, 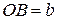 и их длины, при этом
и их длины, при этом 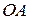 - большая полуось,
- большая полуось, 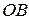 - малая полуось.
- малая полуось.
В случае 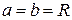 уравнение (1) принимает вид
уравнение (1) принимает вид 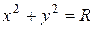 и определяет окружность радиуса
и определяет окружность радиуса 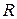 с центром в начале координат.
с центром в начале координат.
Определение 3. Эксцентриситетом эллипса называется выражение 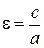 .
.
Так как для эллипса 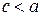 , то
, то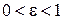 (для окружности
(для окружности 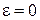 , так как
, так как 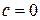 ).
).
Учитывая, что 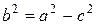 , получаем
, получаем 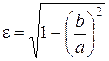 ,
, 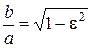 .
.
Из этих уравнений следует, что эксцентриситет характеризует форму эллипса: чем больше эксцентриситет, тем более вытянут эллипс. При 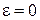 получаем
получаем 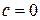

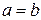 , т.е. получаем окружность.
, т.е. получаем окружность.
Определение 4.Фокальными радиусами точки 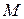 эллипса называются отрезки прямых, соединяющих эту точку с фокусами
эллипса называются отрезки прямых, соединяющих эту точку с фокусами 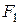 и
и 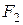 данного эллипса. Их длины определяются формулами:
данного эллипса. Их длины определяются формулами: 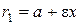 ,
, 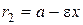 .
.
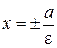 - уравнения директрис эллипса (директриса – от лат. Directrux – направляющая).
- уравнения директрис эллипса (директриса – от лат. Directrux – направляющая).
Пример 2. Найти полуоси, фокусы и эксцентриситет эллипса 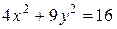 .
.
Решение. Поделив обе части уравнения на 16, получим каноническое уравнение эллипса 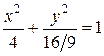 .
.
Из этого уравнения находим 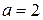 ,
, 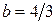 ,
, 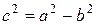 =4-
=4-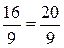


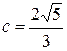 ,
, 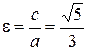 ,
, 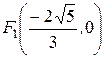 ,
, 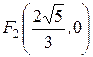 .
.
4.4.3. Гипербола
Определение 5. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная, не равная нулю и меньшая, чем расстояние между фокусами.
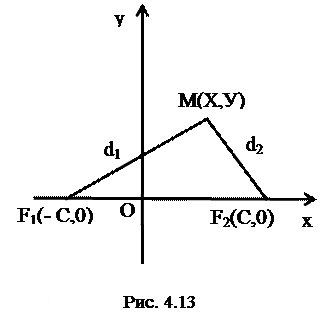 Как и при выводе уравнения эллипса, выберем прямоугольную декартову систему координат так, чтобы фокусы
Как и при выводе уравнения эллипса, выберем прямоугольную декартову систему координат так, чтобы фокусы 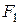 и
и 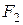 находились на оси
находились на оси 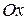 на одинаковом расстоянии
на одинаковом расстоянии 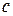 от начала координат (Рис. 4.13).
от начала координат (Рис. 4.13).
Тогда, согласно определению 5, можно записать:
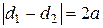 , где
, где 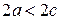 .
.
Повторяя выкладки, аналогичные тем, что были проделаны при выводе уравнения эллипса, получим каноническое уравнение гиперболы
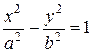 , (2)
, (2)
где 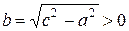 . Исследуем форму кривой, описываемой уравнением (2).
. Исследуем форму кривой, описываемой уравнением (2).
Из уравнения (2) видно, что гипербола является кривой, симметричной относительно осей 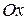 и
и 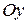 . При этом начало координат является центром симметрии гиперболы.
. При этом начало координат является центром симметрии гиперболы.
Найдем вершины гиперболы – точки пересечения ее с осями 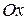 и
и 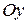 .
.
Положив 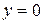 из уравнения (2), находим
из уравнения (2), находим 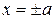 . Значит, точка
. Значит, точка  и
и 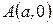 являются вершинами гиперболы, лежащими на оси
являются вершинами гиперболы, лежащими на оси 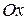 .
.
При 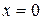 уравнение
уравнение 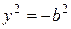 , следующее из (2), не имеет действительных корней. Поэтому точки пересечения гиперболы с осью
, следующее из (2), не имеет действительных корней. Поэтому точки пересечения гиперболы с осью 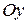 отсутствуют. Вследствие этого ось
отсутствуют. Вследствие этого ось 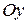 иногда называют мнимой осью симметрии.
иногда называют мнимой осью симметрии.
Запишем уравнение (2) в виде 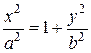 . Так как
. Так как 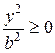 , то
, то 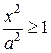
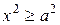 . Значит, все точки гиперболы располагаются правее линии
. Значит, все точки гиперболы располагаются правее линии 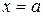 и левее линии
и левее линии 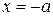 (рис. 4.14).
(рис. 4.14).
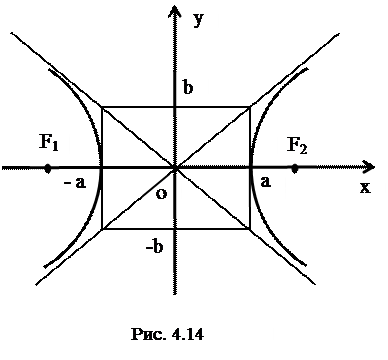 Выясним ход кривой в первой четверти плоскости
Выясним ход кривой в первой четверти плоскости  . Полагая
. Полагая  ,
,  , из уравнения (2) находим
, из уравнения (2) находим 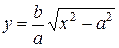 ,
, 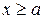 .
.
Отсюда получаем, что при увеличении 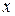 ордината
ордината 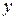 монотонно возрастает от наименьшего значения
монотонно возрастает от наименьшего значения 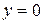 . Если
. Если 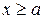 , то слагаемым
, то слагаемым 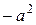 под корнем можно пренебречь. При этом гипербола приближенно описывается линейным уравнением
под корнем можно пренебречь. При этом гипербола приближенно описывается линейным уравнением 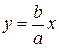 , определяющим прямую, проходящую через начало координат с угловым коэффициентом
, определяющим прямую, проходящую через начало координат с угловым коэффициентом 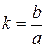 .
.
Однако, при любых 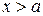 имеем
имеем 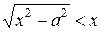 . Это означает, что при возрастании
. Это означает, что при возрастании 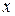 гипербола лишь приближается к прямой
гипербола лишь приближается к прямой 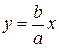 . Прямая
. Прямая 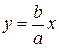 называется наклонной асимптотой гиперболы.
называется наклонной асимптотой гиперболы.
Ход гиперболы в остальных четвертях плоскости 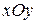 определяем, руководствуясь свойством симметрии.
определяем, руководствуясь свойством симметрии.
Помимо прямой 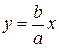 наклонной асимптотой гиперболы является и прямая
наклонной асимптотой гиперболы является и прямая 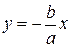 . Обе асимптоты совпадают с диагоналями прямоугольника со сторонами
. Обе асимптоты совпадают с диагоналями прямоугольника со сторонами 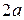 и
и 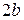 , параллельными осям
, параллельными осям 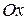 и
и 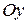 соответственно (рис.4.14).
соответственно (рис.4.14).
Определение 6.Эксцентриситетом гиперболы называется выражение 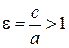 .
.
Приняв во внимание формулу 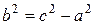 , получим
, получим
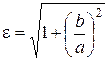 ,
, 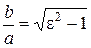 .
.
Следовательно, эксцентриситет гиперболы характеризует форму основного прямоугольника и форму самой гиперболы.
Определение 7.Фокальными радиусами точки 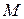 гиперболы называются отрезки, соединяющие эту точку с фокусами данной гиперболы. Их длины
гиперболы называются отрезки, соединяющие эту точку с фокусами данной гиперболы. Их длины 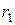 ,
, 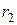 выражаются формулами
выражаются формулами 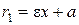 ,
, 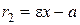 для правой ветви гиперболы и
для правой ветви гиперболы и 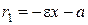 ,
, 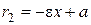 - для ее левой ветви.
- для ее левой ветви.
Определение 8.Директрисами гиперболы называются прямые 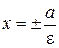 .
.
Поскольку для гиперболы 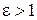 , то
, то 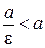 , что означает, что директрисы гиперболы не имеют с ней общих точек.
, что означает, что директрисы гиперболы не имеют с ней общих точек.
Гиперболы 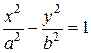 ,
, 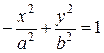 называются сопряженными.
называются сопряженными.
Гипербола с равными полуосями 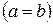 называется равносторонней, ее уравнение
называется равносторонней, ее уравнение 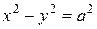 .
.
Пример 3. Найти полуоси, координаты фокусов, эксцентриситет, уравнения асимптот и директрис гиперболы 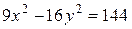 .
.
Решение. Разделив обе части уравнения на 144, получим каноническое уравнение гиперболы
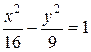 .
.
Из этого уравнения получаем
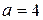 ,
,  ,
, 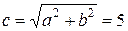 ,
, 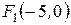 ,
, 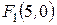 ,
, 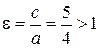 ,
,
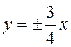 - уравнения асимптот,
- уравнения асимптот, 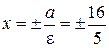 - уравнения директрис.
- уравнения директрис.
4.4.4. Парабола
Определение 9.Параболой называется множество точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).
 Пусть
Пусть 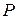 - расстояние от фокуса
- расстояние от фокуса 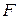 до директрисы
до директрисы 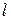 . Ось
. Ось 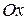 прямоугольной декартовой системы координат выберем так, чтобы она проходила через
прямоугольной декартовой системы координат выберем так, чтобы она проходила через 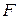 перпендикулярно
перпендикулярно 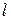 , ее положительное направление от
, ее положительное направление от 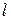 к
к 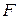 (рис. 4.15), начало координат поместим в середине отрезка
(рис. 4.15), начало координат поместим в середине отрезка 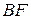 , где
, где 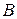 - точка пересечения
- точка пересечения 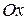 и
и 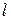 . В этой системе координат
. В этой системе координат 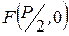 ,
, 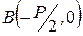 .
.
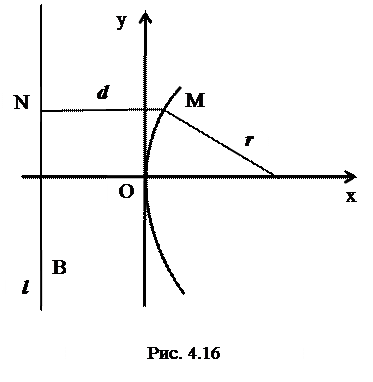 Возьмем произвольную точку
Возьмем произвольную точку 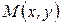 параболы, обозначим через
параболы, обозначим через 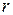 расстояние до фокуса, через
расстояние до фокуса, через 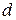 - расстояние до директрисы. По определению 9
- расстояние до директрисы. По определению 9 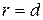 . Поскольку
. Поскольку 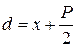 ,
, 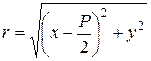 , то
, то 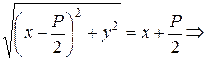
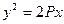 (3) - каноническое уравнение параболы.
(3) - каноническое уравнение параболы.
Из уравнения (3) следует, что 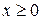 (так как Р > 0), т.е. парабола лежит целиком справа от оси
(так как Р > 0), т.е. парабола лежит целиком справа от оси 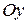 . Парабола симметрична относительно оси
. Парабола симметрична относительно оси 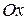 (так как
(так как 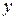 входит в уравнение (3) только
входит в уравнение (3) только
во второй степени); когда 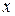 неограниченно возрастает,
неограниченно возрастает, 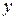 также неограниченно возрастает. Дуга параболы, для которой
также неограниченно возрастает. Дуга параболы, для которой 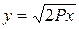 , изображена на рис. 4.15, дуга всей параболы – на рис. 4.16.
, изображена на рис. 4.15, дуга всей параболы – на рис. 4.16.
Уравнение директрисы 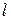 имеет вид
имеет вид 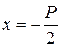 . Если каноническое уравнение параболы имеет вид
. Если каноническое уравнение параболы имеет вид 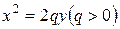 , то парабола будет симметрична относительно оси
, то парабола будет симметрична относительно оси  (рис.4.17).
(рис.4.17).
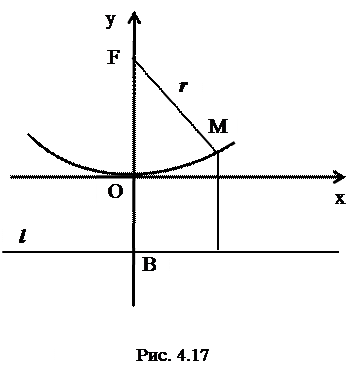 Точка
Точка  - вершина параболы, ось симметрии
- вершина параболы, ось симметрии 
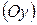 - ось параболы.
- ось параболы.
Геометрический смысл параметра 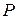 заключается в том, что он характеризует "ширину" области, ограниченной параболой.
заключается в том, что он характеризует "ширину" области, ограниченной параболой.
Пример 4. Найти координаты фокуса и уравнение директрисы параболы 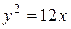 . Определить расстояние точки
. Определить расстояние точки 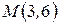 до фокуса.
до фокуса.
Решение.
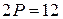 ,
, 
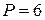 ,
, 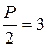 .
.
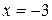 - уравнение директрисы,
- уравнение директрисы, 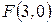 - фокус,
- фокус, 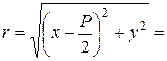
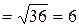 .
.
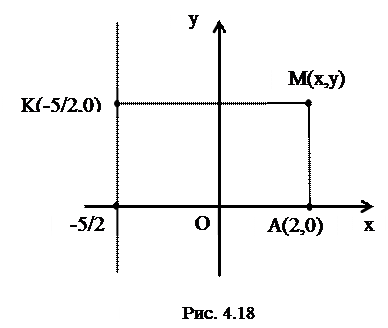
Пример 5. Составить уравнение и построить линию, расстояние каждой точки которой от точки 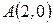 и от прямой
и от прямой 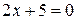 относятся как
относятся как 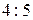 .
.
Решение. Пусть 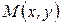 - текущая точка линии в прямоугольных декартовых координатах,
- текущая точка линии в прямоугольных декартовых координатах, 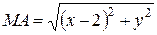 ,
,
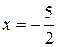 - заданная прямая.
- заданная прямая.
По условию задачи 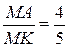 (рис. 4.18), где
(рис. 4.18), где 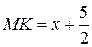 .
.
Отсюда 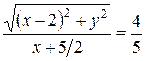 .
.
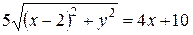

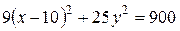


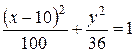 .
.
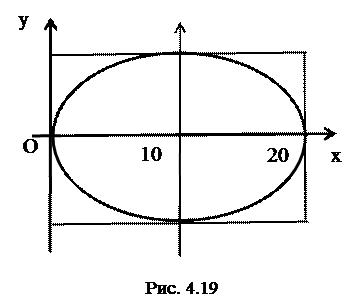
Получим эллипс с центром в точке 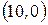 ,
, 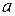 =10,
=10, 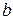 =6 (рис.4.19).
=6 (рис.4.19).
4.5 Полярная система координат
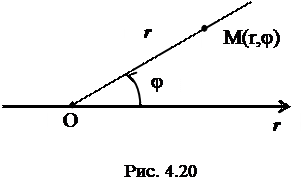 Наряду с прямоугольной декартовой системой координат на плоскости часто используется полярная система, которая вводится с помощью полярной оси (начало ее называется полюсом) и угла поворота оси (положительным считается направление против часовой стрелки) (рис.4.20).
Наряду с прямоугольной декартовой системой координат на плоскости часто используется полярная система, которая вводится с помощью полярной оси (начало ее называется полюсом) и угла поворота оси (положительным считается направление против часовой стрелки) (рис.4.20).
 главные значения полярных координат.
главные значения полярных координат.
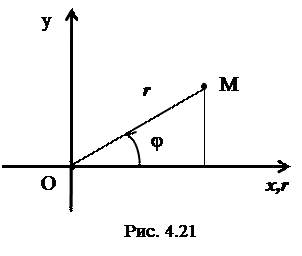 Установим связь между полярными и прямоугольными декартовыми координатами. Пусть эти системы совмещены (рис.4.21).
Установим связь между полярными и прямоугольными декартовыми координатами. Пусть эти системы совмещены (рис.4.21).
Из рис.4.21 следует: 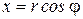 ,
,
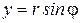 ,
, 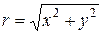 ,
, 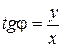 .
.
Рассмотрим теперь в полярных координатах некоторые линии.

Луч. Пусть луч выходит из полюса под углом 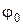 , тогда его уравнение имеет вид
, тогда его уравнение имеет вид 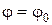 (рис.4.22).
(рис.4.22).
Окружность. Пусть центр окружности радиуса 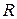 находится в полюсе. Уравнение такой окружности, очевидно, имеет вид
находится в полюсе. Уравнение такой окружности, очевидно, имеет вид 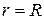 (рис.4.23а).
(рис.4.23а).
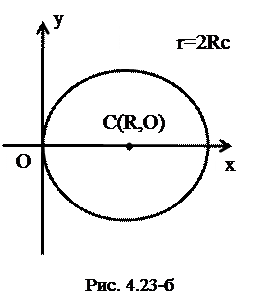 Окружность радиуса
Окружность радиуса 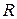 с центром,
с центром,
 смещенным по оси абсцисс вправо на
смещенным по оси абсцисс вправо на  единиц (рис.4.23б):
единиц (рис.4.23б): 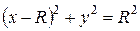

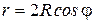 .
.
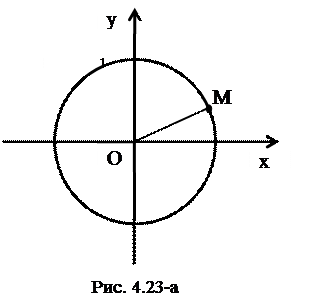
Окружность радиуса 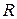 с центром, смещенным по оси ординат вверх на
с центром, смещенным по оси ординат вверх на 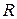 единиц (рис. 4.23в):
единиц (рис. 4.23в):
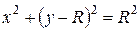

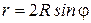 .
.
Линии второго порядка (эллипс, гипербола, парабола).
Уравнение эллипса, гиперболы и параболы в полярной системе координат имеет вид:
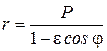 ,
,
где 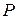 - периметр,
- периметр, 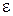 - эксцентриситет.
- эксцентриситет.
При 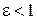 получаем эллипс (полюс совпадает с левым фокусом эллипса); при
получаем эллипс (полюс совпадает с левым фокусом эллипса); при 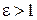 получаем гиперболу (полюс совпадает с правым фокусом гиперболы); при
получаем гиперболу (полюс совпадает с правым фокусом гиперболы); при 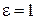 получаем параболу (во всех случаях полярная ось сонаправлена с горизонтальной осью кривой).
получаем параболу (во всех случаях полярная ось сонаправлена с горизонтальной осью кривой).
Чтобы перейти к прямоугольным декартовым координатам, полагаем 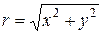 ,
, 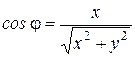 .
.
Подставив эти значения в уравнение, получим после упрощения уравнения эллипса, гиперболы и параболы в прямоугольной декартовой системе координат.
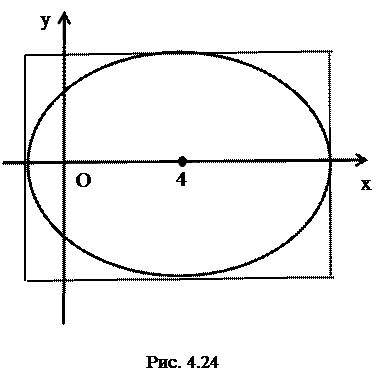
Пример. Определить, какая линия задана уравнением 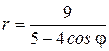 . Записать в декартовых координатах уравнение этой линии и построить ее.
. Записать в декартовых координатах уравнение этой линии и построить ее.
Решение. Преобразуем уравнение к виду 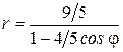 .
.
 Так как
Так как 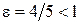 , то получили уравнение эллипса в полярных координатах. Чтобы записать это уравнение в прямоугольных декартовых координатах, воспользуемся формулами
, то получили уравнение эллипса в полярных координатах. Чтобы записать это уравнение в прямоугольных декартовых координатах, воспользуемся формулами
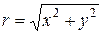 ,
, 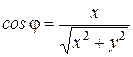 .
.
Получим: 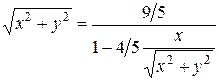

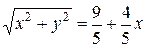


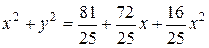

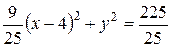


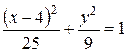 .
.
Получили уравнение эллипса с центром в точке  ,
, 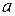 =5,
=5, 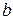 =3 (Рис. 4.24).
=3 (Рис. 4.24).
Розы.
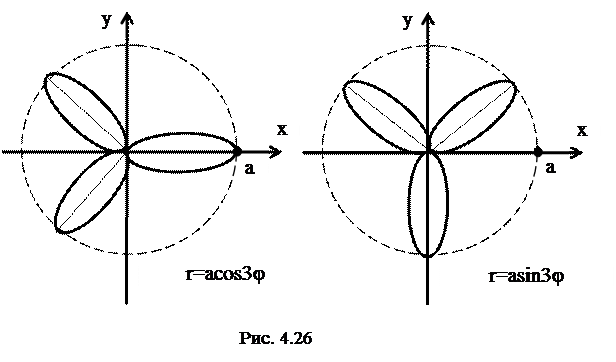
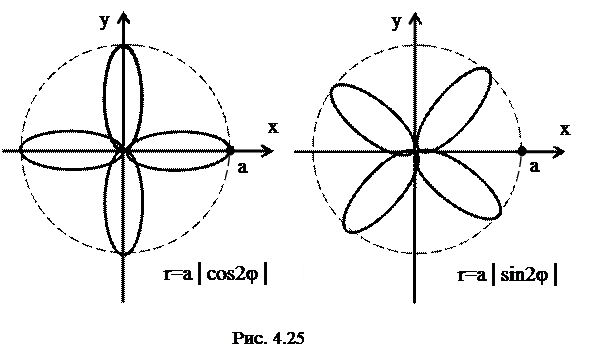
Розами называют семейство кривых, уравнение которых в полярных координатах записывается в виде 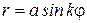 или
или 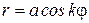 , где
, где 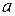 ,
, 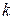 - положительные числа.
- положительные числа.
При любых 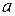 ,
, 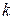 ,
, 
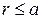 , поэтому можно сделать вывод, что все кривые располагаются внутри круга радиуса
, поэтому можно сделать вывод, что все кривые располагаются внутри круга радиуса 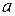 . Вследствие периодичности функций
. Вследствие периодичности функций 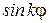 и
и 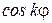 розы состоят из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен
розы состоят из одинаковых лепестков, симметричных относительно наибольших радиусов, каждый из которых равен 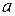 . Количество лепестков розы зависит от значения
. Количество лепестков розы зависит от значения 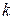 . Если
. Если 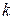 - целое число, роза состоит из
- целое число, роза состоит из 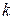
лепестков при нечетном 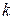 и из 2
и из 2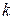 лепестков при четном
лепестков при четном 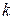 . Если
. Если 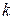 =2, то получаем четырехлепестковые розы, отличающиеся друг от друга расположением на плоскости, причем роза
=2, то получаем четырехлепестковые розы, отличающиеся друг от друга расположением на плоскости, причем роза 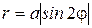 может быть получена из розы
может быть получена из розы 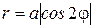 поворотом ее на угол
поворотом ее на угол 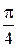 (рис. 4.25).
(рис. 4.25).
Если 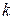 =3, то получаем трехлепестковые розы, причем роза
=3, то получаем трехлепестковые розы, причем роза 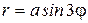 получается из розы
получается из розы 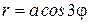 поворотом ее на угол
поворотом ее на угол 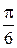 (рис. 4.26).
(рис. 4.26).
Спирали.
Спираль Архимеда определяется как траектория точки, участвующей одновременно в двух равномерных движениях, одно из которых осуществляется вдоль прямой, а другое – по окружности.
Полярное уравнение спирали Архимеда имеет вид 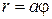
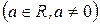 . Так как
. Так как 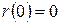 ,
, 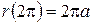 , то линия незамкнута, причем
, то линия незамкнута, причем 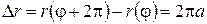 . Эта разность не зависит от
. Эта разность не зависит от 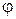 . Следовательно, имея виток линии, можно построить всю спираль Архимеда (рис.4.27).
. Следовательно, имея виток линии, можно построить всю спираль Архимеда (рис.4.27).
Логарифмическая спираль – это линия с уравнением 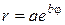 ,
,  . Она пересекает все свои радиусы – векторы под одним и тем же углом. Это дает возможность сохранять постоянный угол резания для вращающихся ножей,
. Она пересекает все свои радиусы – векторы под одним и тем же углом. Это дает возможность сохранять постоянный угол резания для вращающихся ножей,
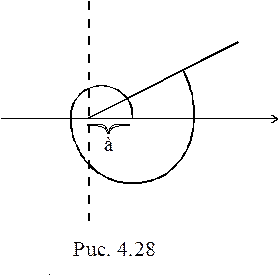
выполненных по логарифмической спирали (рис. 4.28). Такую же форму имеют зубья циркулярных пил, зубки режущих частей горных добычных комбайнов.
Кардиоида
 Кардиоида – это линия с уравнением (от греч. kardia – сердце и eidos – вид).
Кардиоида – это линия с уравнением (от греч. kardia – сердце и eidos – вид).
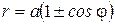
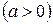 или
или
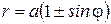
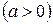 (рис. 4.29)
(рис. 4.29)
Лемниската Бернулли (лемниската – от лат. lemniskatus – украшенный лентами).
Лемниската Бернулли – это линия с уравнением 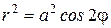
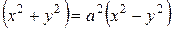 (рис.4.30).
(рис.4.30).
 В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого размера, как это имеет место на железнодорожных линиях, в горной местности и на трамвайных путях.
В технике лемниската применяется, в частности, в качестве переходной кривой на закруглениях малого размера, как это имеет место на железнодорожных линиях, в горной местности и на трамвайных путях.
4.6. Параметрические уравнения линий
Множество точек М(х,у) плоскости, координаты которых удовлетворяют уравнениям х=х(t). y=y(t), t Є T, параметрически задаёт некоторую линию.
Рассмотрим параметрическое задание некоторых линий.
1. Прямая у = кх + b 
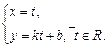
2. Окружность с центром в начале координат и радиусом, равным R
х2 + у 2 = R 2
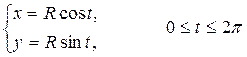
Здесь параметр t – угол между положительным направлением оси Ох и радиусом – вектором  текущей точки М(х,у) окружности.
текущей точки М(х,у) окружности.
3. Эллипс. 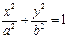
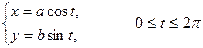
4. Парабола. у 2 = 2pх 
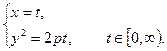
 В частности
В частности
у = х 2
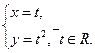
5. Гипербола 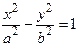
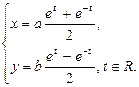
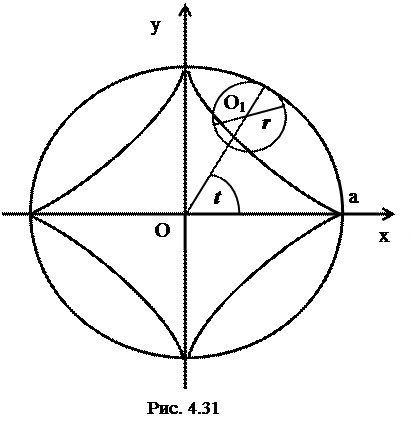
6. Астроида (от греческого astron-звезда и eidos – вид) (рис.4.31) – замкнутая линия, являю-щаяся траекторией точки, лежащей на окружности круга радиусом 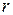 , который катится по внутренней стороне неподвижного круга радиуса
, который катится по внутренней стороне неподвижного круга радиуса 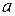
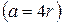 . Ее уравнение имеет вид
. Ее уравнение имеет вид
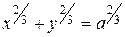
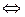
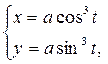 0 ≤ t < 2π
0 ≤ t < 2π
7. Циклоида (от греческого kykloeides – кругообразный) (рис.4.32) – это кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии.
 Циклоида состоит из равных дуг, каждая из которых соответствует полному обороту катящегося круга. Параметрические уравнения циклоиды:
Циклоида состоит из равных дуг, каждая из которых соответствует полному обороту катящегося круга. Параметрические уравнения циклоиды:
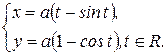
К контрольной работе К содержанию
 2014-02-09
2014-02-09 953
953