1. Функция распределения принимает значения из промежутка [0, 1], т.е.
0 ≤ F (x) ≤ 1.
Это свойство следует из определения функции распределения.
2. Если х2 >х1, то
3.
P (x 1≤ X < x 2 ) = F (x 2)- F (x 1). (1)
Доказательство. Представим событие, состоящее в том, что случайная величина примет значение, меньшее х 2, в виде суммы несовместных событий –
{w: X (w) < x 2} = {w: X (w)< х 1} È {w: x 1 ≤ X (w) < x 2}.
Так как события несовместные, применим аксиому 3 –
P (X < x 2) = P (X < x 1) + P (x 1 ≤ X < x 2),
но P (X < x 2) = F (x 2), P (X < x 1) = F (x 1), следовательно
F (x 2) = F (x 1) + P (x 1 ≤ X < x 2), (2)
а это и означает, что P (x 1≤ X < x 2 ) = F (x 2)– F (x 1).
4. Функция распределения – неубывающая функция, т.е. если
x 2 > x 1 => F (x 2) ≥ F (x 1).
Доказательство. Если x 2 > x 1, то справедливо соотношение (2). Но, согласно
аксиоме 1 P(x 1 ≤ X < x 2) ≥ 0,
следовательно, F (x 2) ≥ F (x 1).
5. P (X ≥ x) = 1- F (x).
Доказательство. События {w: X (w) ≥ x} и {w: X (w) < x } – противоположные события, так как они несовместные и
{w: X (w) ≥ x }È{w: X (w) < x } = Ω, следовательно,
Р {w: X (w) ≥ x } + Р {w: X (w) < x }=1, тогда Р (X (w) ≥ x) = 1– Р (X (w) < x) = 1 – F (x).
6. Если х ® ¥, то 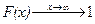 .
.
Доказательство. Пусть x 1, …, x n …– бесконечно возрастающая числовая последовательность, xn → ∞ при n → ∞, надо доказать, что 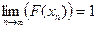 .
.
Рассмотрим последовательность несовместных событий А 1, А 2, …, А n, …
А 1 = {w: X (w)< x 1}, А 2 = {w: x 1 ≤ X (w) < x 2}, …, A n = {w: x n-1 ≤ X (w) < x n}, n = 3, 4, …
Очевидно, что событие {w: X (w) < x n} можно представить в виде суммы событий А 1, А 2, …, А n
{w: X (w) < x n}= 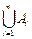 .
.
Так как события Ai несовместны, то по аксиоме сложения
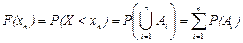 .
.
Легко видеть, что событие, равное сумме всех событий Аi, является достоверным событием, т.е.
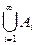 = Ω.
= Ω.
Тогда по аксиоме 2 и аксиоме 3` имеем
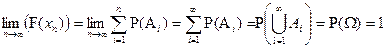 .
.
Замечание. Мы не пишем 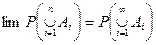 , так как не определен предельный переход под знаком вероятности.
, так как не определен предельный переход под знаком вероятности.
6. Если x → - ∞, то F (x) → 0.
7. Функция распределения непрерывна слева, т.е. 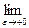
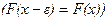 .
.
Свойства 6, 7 можно доказать при помощи аксиомы непрерывности, которая является альтернативной по отношению к аксиоме 3`. То есть в аксиоматику теории вероятностей вместо аксиомы 3` можно включить аксиому непрерывности, тогда аксиому 3` можно будет доказать как теорему и наоборот, аксиому непрерывности можно доказать с использованием аксиомы 3`.
Аксиома непрерывности. Пусть A 1, A 2,.., An, … – последовательность событий из S, причём A 1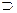 A 2
A 2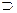 A 3
A 3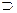 …
…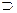 An
An 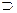 … и
… и 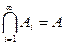 , тогда
, тогда 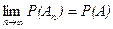 .
.
Доказательство свойства 6. Рассмотрим произвольную бесконечно убывающую монотонную последовательность
x1 > x2 >…> xn >…, причём xn →-∞, n →∞.
Рассмотрим последовательность событий A 1, …, An, …, Аn ={w: (Х < хn) }. По определению Р (Аn) = Р (Х< хn) = F (хn). Очевидно, что последовательность событий A1, A2,..., An удовлетворяет условиям аксиомы непрерывности:
A 1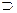 A 2
A 2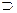 A 3
A 3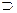 …
…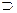 An
An 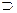 … и
… и 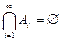 .
.
Тогда, 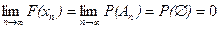 , следовательно
, следовательно
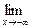
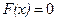 .
.
График функции распределения F(x) изображен на рис.1.

Рис.1.
Приведем доказательство аксиомы непрерывности. Пусть даны события A 1, A 2,..., An, … и A 1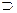 A 2
A 2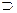 A 3
A 3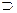 …
…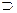 An
An 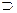 … и
… и 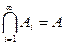 .
.
Тогда, перейдя к противоположным событиям, получим
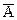 1 Ì
1 Ì 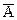 2 Ì
2 Ì 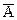 3 Ì….
3 Ì….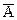 n Ì ….,
n Ì …., 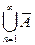 n =
n =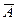 .
.
Представим события 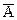 и
и 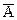 n в виде сумм несовместных событий
n в виде сумм несовместных событий
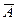 n =
n = 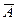 1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn)
1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn)
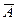 =
= 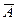 1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn) È…
1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn) È…
Убедиться в правильности этих равенств можно при помощи диаграмм Эйлера–Вена.
Используя расширенную аксиому сложения, получим
Р(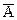 ) = Р(
) = Р(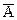 1) + Р(А1\А2) + Р(А2\А3) +…+ Р(Аn-1\Аn) +…=
1) + Р(А1\А2) + Р(А2\А3) +…+ Р(Аn-1\Аn) +…=
=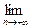 (Р(
(Р(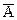 1) + Р(А1\А2) + Р(А2\А3) +…+ Р(Аn-1\Аn)) =
1) + Р(А1\А2) + Р(А2\А3) +…+ Р(Аn-1\Аn)) =
=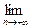 Р(
Р(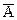 1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn)) =
1 È (А1\А2) È (А2\А3) È…È (Аn-1\Аn)) =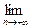 Р(
Р(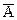 n).
n).
Следовательно, Р(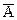 ) =
) = 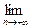 Р(
Р(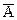 n), но Р(А) = 1–Р(
n), но Р(А) = 1–Р(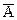 ), тогда Р(А) = 1–Р(
), тогда Р(А) = 1–Р(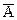 ) =
) =
=1–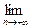 Р(
Р(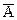 n) =
n) = 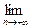 (1–Р(
(1–Р(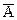 n)) =
n)) = 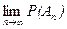 , т.е. получили, что
, т.е. получили, что 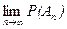 = Р(А).
= Р(А).
 2014-02-18
2014-02-18 377
377








