Лекция 5. Распределения дискретных случайных величин

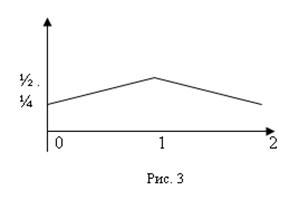
Дискретная случайная величина принимает конечное или счётное множество значений. Пусть Х – дискретная случайная величина, принимающая значения x₁ < x₂ < …< x_n … с вероятностями р₁, р₂, …., р_n,…, Р(x_i) = p_i, 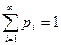. Если по оси абсцисс отложить x₁, x₂, …, x_n …, а по оси ординат – соответствующие вероятности p_i и соединить соседние точки отрезками, то получим многоугольник распределения дискретной случайной величины (рис.1), который является графическим изображением ряда распределения дискретной случайной величины. Например, если Х – число выпадений «решки» при двух подбрасываниях монеты, то ряду распределения, изображенному на рис. 2 будет соответствовать многоугольник распределения, изображенный на рис. 3.

Рис. 1 Рис.2

Рассмотрим, что представляет собой функция распределения дискретной случайной величины Х.

Если х £ х₁, то F (x) = P (X< x)= 0, так как событие {w: X< x } – невозможное.

Если х₁ < х £ х₂, то событие {w: X< x } наступит тогда и только тогда, когда наступит событие {w: X = x₁ }, поэтому F (x) = P (X< x) = Р { X = x₁ } = р₁.

Если х₂ < х £ х₃ , то событие {w: X< x } равно сумме событий {w: X = x₁ }и {w: X = x₂ }. Поэтому F (x) = P (X< x) = Р { X = x₁ } + Р { X = x₂ } = р₁ + р₂.

Аналогично, если х_i < х £ х_i+1, то F (x) = р₁ +р₂+…+р_i.

Таким образом, функция распределения дискретной случайной величины имеет вид

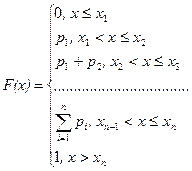
Очевидно, что функция распределения дискретной случайной величины постоянна на промежутках (-¥, х₁ ], (х₁, х₂ ], …, (х_i, х_i+1 ], … В точках x₁, x₂, …, x_n …, функция распределения имеет скачки, равные вероятности того, что случайная величина примет соответствующее значение. График функции распределения будет иметь вид, схематично изображенный на рис. 4. График функции распределения, соответствующий ряду распределения числа выпадений «решки», изображен на рис. 5.

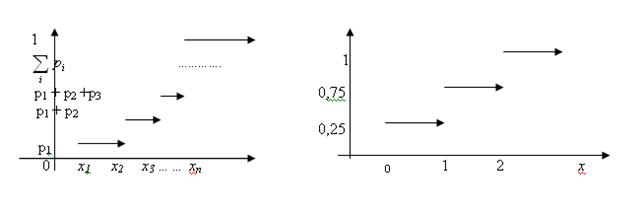
Рис. 4 Рис. 5