2014-02-18
462
Определение 6. Случайная величина Х имеет распределение Бернулли, если P (Х = m) = Pm = pmqn-m, m = 0, 1, …, n.
При больших m и n становится проблематичным вычисление по формуле Бернулли. Поэтому в ряде случаев удается заменить формулу Бернулли подходящей приближенной асимптотической формулой. Так если n – велико, а р мало, то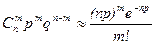 
.
Теорема Пуассона. Если n ® ¥, а p ® 0, так что np ® l, то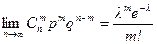 
.
Доказательство. Обозначим ln = np, по условию теоремы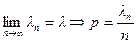 
, тогда
.
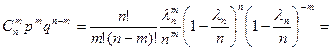
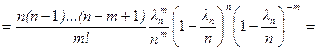
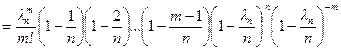При n ® ¥, l nm ® l m,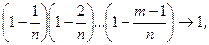 
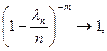
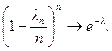
Отсюда получаем утверждение теоремы. Рn (m) ® 
при n ® ¥.
Формула Пуассона хорошо приближает формулу Бернулли, если npq £ 9. Если же произведение npq велико, то для вычисления Рn(m) используют локальную теорему Муавра–Лапласа.
Локальная теорема Муавра – Лапласа. Пусть p Î(0;1) постоянно, величина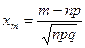 
равномерно ограничена, т.е. $ с, |xm|<с. Тогда
,
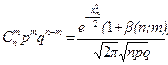где b(n;m) – бесконечно малая величина, причем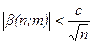 
.
Из условий теоремы следует, что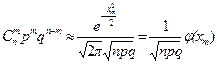 
,
где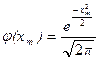 
, .
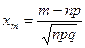Для вычисления Рn(m) по формуле, приведенной рнее, используют таблицы функции
.
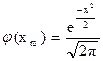Задача 1. В магазин одежды один за другим входят трое посетителей. По оценкам менеджера, вероятность того, что вошедший посетитель совершит покупку, равна 0,3. Составить ряд числа посетителей, совершивших покупку.
