2014-02-18
1200
Напор
Рассмотрим точку К (рис. 6) на произвольной глубине h по отношению к плоскости сравнения 0 – 0. В точке К установим пьезометр. Пьезометрический напор
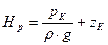
где 
– геометрический напор.
Аналогично определим напор в точке С:
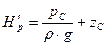
Очевидно, что 
.
Отсюда следует, что напор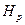 
состоит из удельной потенциальной энергии давления 
и удельной потенциальной энергии положения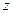 
(геометрический напор).
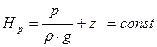
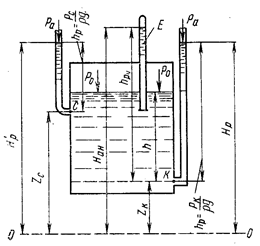
Рис 6. Схема расчета напора
Далее опустим в сосуд на малую глубину трубку Е, предварительно выкачав из нее воздух. По этой трубке жидкость поднимается на высоту 
равную приведенной пьезометрической высоте. Сумма двух линейных величин и называют гидростатическим напором:
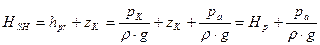(19)
Таким образом, при учете гидростатического напора учитывают атмосферное давление
.
Пусть в точке К (рис. 6) имеется частица жидкости массой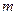 
. Потенциальная энергия этой массы относительно плоскости 0-0 равна 
.
С учетом полной высоты добавится еще 
- пьезометрическая высота и полная потенциальная энергия частицы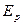 
будет
(20)
Разделив обе части уравнения на 
, получим уравнение для удельной потенциальной энергии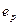 
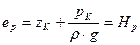(21)
Итак, удельная потенциальная энергия жидкости равна пьезометрическому напору и для всех точек на оси К рассматриваемого объема одинакова.
