Определение видимости отрезка относительно наблюдателя

За направление плоскости возьмем такое, при котором скалярное произведение ее на точку наблюдения дает положительный результат. Если после определения коэффициентов плоскости (например, методом Ньюэла) скалярное их произведение на точку наблюдения 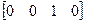, расположенную в бесконечности на положительной полуоси Z дает "-", то необходимо умножить коэффициенты плоскости на "-1".

Такое направление нормали плоскости позволяет использовать следующее правило для определения видимости концов отрезка: если скалярное произведение конца отрезка на столбец коэффициентов плоскости положительно, то эта вершина видима.

* Если скалярное произведение 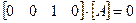, то исходная плоскость является фронтально - проецирующей.

Пример

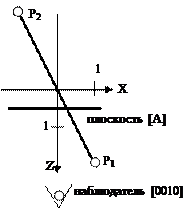Заданы:

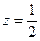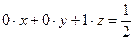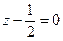- плоскость или ,

или 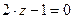, т.е.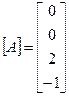

- отрезок [P₁P₂], где P₁=[1, 0, 2, 1], P₂=[-1, 0, -2, 1].

1. Проверка уравнения плоскости на направление нормали в сторону наблюдателя.

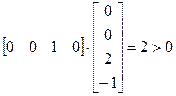
2. Нахождение точки пересечения прямой и плоскости

,

=>

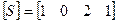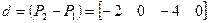
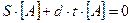
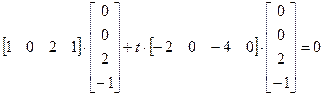
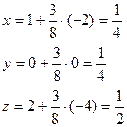
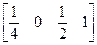– точка пересечения

3. Определение видимости концов отрезка

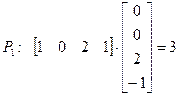=> P₁ – видима

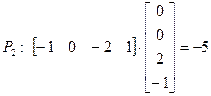=> P₂ – невидим.