Дисперсионное взаимодействие

Индукционное взаимодействие

Когда одна молекула имеет постоянный дипольный момент Р₁, она может навести диполь Р₂ в другой молекуле, если последняя обладает определенной поляризуемостью α:

Р₂ = α ∙ Е₁, (3.7)

где: Р₂ – наведенный диполь; α - коэффициент поляризуемости второй молекулы; Е₁ – локальная напряженность электрического поля в центре поляризуемой молекулы, создаваемая постоянным диполем Р₁ первой молекулы. Поле Е₁ диполя Р₁ на расстоянии r от постоянного диполя равно Е₁ = 2 ∙ Р₁ / r³, если Р₁ и r расположены параллельно. Отсюда можно заключить, что энергия индукционного взаимодействия (U_ИНД), усредненная по всем ориентациям постоянного диполя Р₁, равна

U_ИНД = − Е₁² / 2 = 2 ∙ α² ∙ Р₁² / r⁶. (3.8)

Смещение электронов в одну сторону при поляризации молекулы соседним диполем компенсируется их смещением в противоположную сторону за счет действия такого же постоянного диполя с обратно направленным моментом, который расположен по другую сторону молекулы. Поскольку в жидких и твердых телах поляризуемая молекула испытывает симметричное влияние большого количества соседних молекул, их результирующее действие в значительной степени компенсируется.

Наиболее распространенным видом слабых взаимодействий является дисперсионное (поляризационное) взаимодействие. Оно наблюдается между молекулами, не обладающими постоянными дипольными моментами. Основная часть данного взаимодействия обусловлена внешними наиболее слабо связанными электронами. Природа дисперсионного взаимодействия носит квантово-механический характер и является результатом появления «мгновенных» диполей, которые возникают при движении электронов в молекулах, не обладающих постоянными дипольными моментами.

В гармоническом приближении движение электрона в молекуле можно рассматривать в виде линейного гармонического осциллятора, энергия которого равна

Е_n = (n + 1/2) ∙ ћ ∙ ω_O (n = 0, 1, 2,…), (3.9)

где: ω_O – частота колебаний электронного осциллятора, вычисляемая по правилам классической механики; n – главное квантовое число, значение которого определяет энергетический уровень электрона, ћ – постоянная Планка. В низшем квантовом состоянии при n = 0 энергия осциллятора не обращается в нуль и равна

Е_О = ћ ∙ ω_O/2. (3.10)

Значение Е_О = ћ ∙ ω_O/2 называется нулевой энергией. Ее существование является следствием соотношения неопределенностей, согласно которому электрон как квантовая частица не может обладать одновременно определенной координатой (х) и импульсом (р). Импульс частицы (р) равен произведению ее массы (m) на скорость (υ): р = m ∙ υ, или Е = р²/2 m. Неопределенности в значениях координаты (∆х) и импульса (∆р) электронов связаны соотношением неопределенностей Гейзенберга:

∆х ∙ ∆р ≈ ћ. (3.11)

Вследствие равенства (3.10) координата и импульс электрона не могут принимать одновременно строго определенные значения, то есть ∆х ≠ 0, ∆р ≠ 0, а это возможно только в том случае, если электрон обладает какой-то минимальной энергией (Е_О = ћ ∙ ω_O/2).

Иными словами, при n = 0 существуют нулевые колебания электрона с энергией Е_О, которые связаны с быстрыми движениями и смещениями заряда из положений равновесия, а значит, с появлением «мгновенных» дипольных моментов в молекуле, которая находится в состоянии покоя. Появление дипольного момента в одной молекуле вызывает возникновение в окружающем пространстве поля и индуцирует дипольный момент в другой молекуле. Взаимодействие быстро меняющихся диполей приводит к тому, что изменение дипольного момента одного осциллятора вызывает добавочную поляризацию в другом, и наоборот. Таким образом, эти два осциллятора оказываются связанными. Если раньше каждый из них колебался с частотой ω_O, то теперь в системе связанных осцилляторов появляются две частоты ω₊ и ω₋, соответствующие симметричным и антисимметричным колебаниям (рис.3.3).

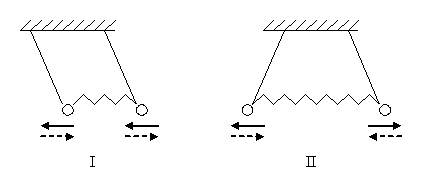
Рис.3.3.Симметричные (I) и антисимметричные (II) колебания связанных маятников.

Энергии связанных осцилляторов имеют дискретные квантовые значения:

Е_n+ = ћ ∙ ω₊ ∙ (n₊ + 1/2); Е_n− = ћ ∙ ω₋ ∙ (n₋ + 1/2) (3.12)

или в нулевом состоянии (при n₊ = n₋ = 0) Е_n+ = ћ ∙ ω₊/2; Е_n− = ћ ∙ ω₋/2, (3.13)

е² е⁴

где: ω₊ = ω_O ∙ (1 − ——— − ————);

r³ ∙ f 2 r⁶ ∙f²

е² е⁴

ω₋ = ω_O ∙ (1 + ——— − ————); f = m ∙ ω_O².

r³ ∙f 2 r⁶ ∙f²

Полная энергия системы связанных осцилляторов будет равна

е⁴

Е = Е_n+ + Е_n− = ћ ∙ ω_O ∙ (1 − ————). (3.14)

2 ∙ r⁶ ∙ f²

При сравнении этого выражения (3.14) с суммой нулевых энергий несвязанных осцилляторов

Е = ћ ∙ ω_O/2 + ћ ∙ ω_O/2 = ћ ∙ ω_O

видно, что полная энергия системы меньше этой суммы на величину, равную е⁴∙ ћ ∙ ω_O / (2 r⁶ ∙ f²), которая и есть энергия связи, или энергия дисперсионного взаимодействия (U_ДИСП):

е⁴∙ ћ ∙ ω_O

U_ДИСП = − ——————. (3.15)

2 ∙ r⁶ ∙ f²

Таким образом, изменение уровней энергии, связанное с появлением мгновенной асимметрии в распределении зарядов, является физической причиной сил межмолекулярного взаимодействия между молекулами, находящимися в основном состоянии. Более строгий расчет дисперсионного взаимодействия дает выражение:

3 ∙ I₁ ∙ I₂ ∙ α₁ ∙ α₂

U_ДИСП = − ————————, (3.16)

2 ∙ (I₁ + I₂) ∙ r⁶

где: I₁, I₂ – ионизационные потенциалы; α₁, α₂ – поляризуемости молекул.

Суммарное ван-дер-ваальсовое взаимодействие двух молекул определяется суммой U_ОР + U_ИНД + U_ДИСП и составляет величину от 4,0 до 13,0 Дж/моль в пересчете на число взаимодействующих пар групп. Эта энергия сравнима с величиной тепловой энергии молекул при комнатной температуре (2,5 кДж/моль).

Существенным отличием дисперсионных сил от ориентационных и индукционных сил является их аддитивность. Это связано с тем, что при одновременном взаимодействии нескольких молекул каждая из них наводит во всех остальных молекулах координированные мгновенные диполи. Эти диполи находятся в фазе с соответствующими возбуждающими диполями. Каждый из этих диполей ориентирован всегда так, что он притягивается к соответствующему индуцирующему диполю. Другие диполи, не находящиеся в фазе с последним, только периодически взаимодействуют с ним и после усреднения по всем возможным фазам дают нулевой вклад в энергию.

На малых расстояниях начинают сказываться силы отталкивания между атомами, которые связаны с эффектами отталкивания электронных облаков при их взаимопроникновении.

Обменные взаимодействия происходят при перекрывании волновых функций электронов, то есть на расстояниях ~ 0,1 нм (то есть длин химических связей), и убывают с расстоянием скорее (~ 1/r²), чем притяжение (~ 1/r⁶) диполей, индуцированных посредством действия электромагнитных полей.

Ван-дер-ваальсовые силы складываются из сил притяжения и отталкивания. Их не рассчитывают строго теоретически, а задают в виде атом-атомных потенциалов Букингема (3.17):

U(r_ik) = − A/r_ik + B ∙ exp (− μ ∙ r_ik), (3.17)

или Леннарда-Джонса (3.18):

U(r_ik) = − A/(r_ik)⁶ + B/(r_ik)¹², (3.18)

где: А, В, μ – константы; r_ik – расстояние между взаимодействующими атомами (i и k). Первые члены уравнений (3.17) и (3.18) соответствуют притяжению, вторые – отталкиванию. Формулы при заданных значениях констант определяют минимальное расстояние r_O, на котором система из двух взаимодействующих атомов устойчива.

Если ограничиться только силами Ван-дер-Ваальса и не принимать во внимание других взаимодействий, то силовое поле вокруг атома обладает центром симметрии. Тогда можно определить эффективный объем вокруг атома, или эффективный радиус взаимодействия, в пределах которого невозможно одновременное нахождение двух атомов. Например, для пары ковалентно-несвязанных атомов С ∙ ∙ ∙ С обычное расстояние составляет 0,32 нм, а минимально возможное 0,3 нм; для атомов С ∙ ∙ ∙ О эти расстояния соответственно составят 0,28 нм и 0,27 нм; для атомов С ∙ ∙ ∙ N 0,29 нм; для атомов Н ∙ ∙ ∙ Н 0,2 нм и 0,19 нм.

Силы Ван-дер-Ваальса лежат в основе формирования ряда биоструктур, например, двуспиральных полинуклеотидов. Упаковка плоских молекул азотистых оснований в вертикальные пачки обеспечивается «вертикальными» (стэкинг) взаимодействиями, в которые дисперсионный член (U_ДИСП) вносит существенный вклад. Например, для стэкинг-взаимодействий пар Г – Ц U_ДИСП = – 39,1 кДж/моль, а значение U_ОТТ = + 18,14 кДж/моль. С учетом водородных связей и электростатического отталкивания суммарное значение энергии взаимодействия в этм случае составит – 27,9 кДж/моль. «Горизонтальные» взаимодействия отвечают за упаковку азотистых оснований в одной плоскости и определяют образование комплементарных пар А – Т и Г – Ц. В этом случае дисперсионные взаимодействия играют меньшую роль, а основной вклад вносит электростатическое притяжение. Например, для пары А – Т U_ДИСП = – 7,18 кДж/моль, U_{ЭЛ-СТАТ} = 19,32 кДж/моль, U_ОТТ = + 16,0 кДж/моль, U_ВОДА = – 2,48 кДж/моль, что в сумме дает ∑ U = 12,01 кДж/моль.