2014-02-18
438
В качестве примера однонаправленной функции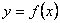 
рассмотрим широко известную функцию дискретного возведения в степень: 
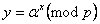, где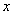 
– целое число от 1 до 
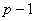включительно, а вычисление производится по модулю 
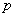, где 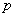– очень большое простое число; 
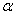– целое число (
).
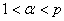Напомним, что простым числом называется целое число, которое не делится ни на какие числа, кроме себя самого и единицы.
Пример 10.1. Для примера возьмем небольшое простое число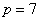 
; тогда для осуществления преобразований можно выбрать примитивный элемент 
, так как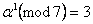 
, 
, 
, 
, 
, 
.
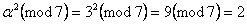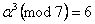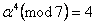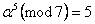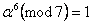Функция 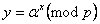вычисляется сравнительно просто, а обратная к ней функция 
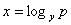является вычислительно сложной практически для всех (
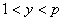) при условии, что не только 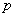велико, но и (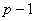) имеет большой простой множитель (лучше всего, если это будет другое простое число, умноженное на 2). В связи с этим такую задачу называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.
Задача дискретного логарифмирования состоит в том, что для известных целых , ,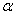 
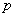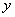необходимо найти целое число 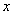. Однако алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.
|
|
|
