Основная идея использования оптимизационных методов заключается в том, что создается математическая модель, отражающая реальную задачу и проводится исследование задачи на этой модели. Математические модели объекта управления могут весьма сильно различаться между собой по размерности, сложности и характеру используемого математического аппарата. Для организационного управления очень важны так называемые оптимальные решения [7]. Эти модели включают две составные части – целевую функцию (критерий оптимальности) и ограничения.
Целевая функция – инструмент, при помощи которого то или иное состояние измеряется с точки зрения эффективности операции. Целевая функция строится таким образом, чтобы оптимальной (наилучшей с точки зрения выбранного критерия) ситуации соответствовало наибольшее (в задачах максимизации) либо наименьшее (в задачах минимизации) значение этой функции. Сама же ситуация определяется набором заданных и управляемых переменных, значения которых мы отыскиваем. Построение критерия оптимальности обычно оказывается весьма трудной задачей. Однако без выбранного и формализованного критерия невозможно ни оценить решение, ни узнать, что какое-то решение действительно является наилучшим.
Вторая часть модели – ограничения – представляет собой математическую запись условий, при которых осуществляется выбор решений. Любое из возможных решений, удовлетворяющих этим условиям, называется допустимым планом. Допустимый план, на котором целевая функция принимает экстремальное значение, называется оптимальным.
После того как модель построена, начинается ее анализ, основной целью которого является нахождение оптимального решения. Однако анализ модели не заканчивается, когда найдено оптимальное решение. Математические модели позволяют проводить эксперименты с экономическими и производственными факторами, являются удобным средством для исследования проблем управления. Характеристика типов математических моделей, используемых в организационном управлении, самая разнообразная.
Математическое программирование. В самом общем виде модель математического программирования может быть представлена следующим образом:
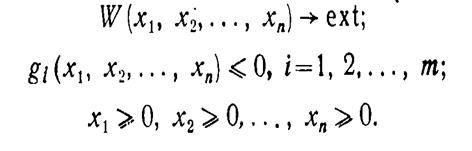
Задача математического программирования в этом случае формулируется так: найти такие элементы решения х1,..., хn, при которых целевая функция W(х1,..., хn) достигает экстремума. Общих методов нахождения экстремума функции W(х) любого вида при наличии произвольных ограничений, накладываемых на х1,..., хn не существует. Однако для случаев, когда функции W(х) и ограничения обладают определенными свойствами, современная теория математического программирования предлагает ряд специальных методов.
Например, если W(х) есть линейная функция и ограничения представлены в виде линейных равенств и неравенcтв, то мы имеем дело с задачей линейного программирования. В общем случае W(х), gi(х), i=1,n являются нелинейными функциями и задача классифицируется как задача нелинейного программиро- вания. Если на переменные х1,..., хn накладываются требования целочисленности, то математическая модель относится к классу задач дискретного программирования. Стохас т и ч е с к им п р о г р а м м и р о в а н и е м называется раздел математического программирования, изучающий методы решения задач управления и планирования в условиях неопределенности. В случае, когда параметры математической модели являются случайными величинами, вероятностные законы распределения которых из-вестны, то решение стохастической модели может быть сведено к решению детерминированной модели. Наиболее трудным для математического программирования является тот случай, когда вероятностное распределение случайных параметров модели неизвестно.
При обосновании решения в условиях неопределенности, чтобы мы ни делали, а элемент неопределенности остается. Поэтому неразумно предъявлять к точности решения таких моделей высокие требования.
Теория оптимального управления. Задачи математического программирования являются статическими по своей природе. Изучение класса динамических моделей осуществляется теорией оптимального управления. На фоне задач математического программирования теория оптимального управления выделяется особым богатством новых идей и методов. Центральной идеей, определяющей развитие теории оптимального управления, была идея оптимизации многошагового решения.
Класс оптимизационных задач оптимального управления не сводится к классическому вариационному исчислению. Выдающуюся роль в развитии прикладного характера теории оптимального управления сыграли работы Р. Беллмана и Л. С. Понтрягина. Первый создал теорию динамического программирования, а второй сформулировал принцип максимума, позволяющий с помощью множителей Лагранжа свести задачу оптимального управления к некоторой специальной задаче математического программирования.
Общая задача теории оптимального управления может быть сформулирована следующим образом: определить векторные значения х(k) и u(k), k=0, 1, 2,..., Т, доставляющие максимум функционалу
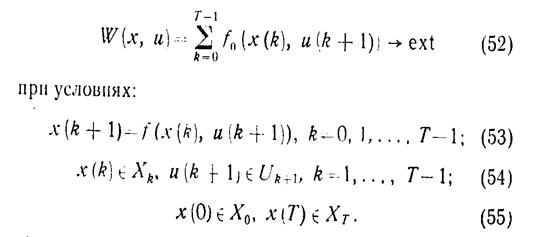
Конкретизация условий (53) – (55) порождает различные типы задач оптимального управления. Управлением условимся называть последовательность векторов (u(k)) = (u(1), u(2),..., u(Т)). Последовательность векторов (х(k)) =(х(0), х(1),..., х(T)) будем называть траекторией системы. Переменные х(k), k=1, 2,..., Топределяются как ф а з о в ы е п е р ем е н н ы е. Соотношение (53) представляет собой уравнение движения системы. Соотношения (54) определяют о г р а н и ч е н и я, накладываемые на траекторию движения и управления системы. Соотношения (55) определяют граничные условия системы. Задачи оптимального управления, так же как и задачи математического программирования, подразделяются на детерминированные и стохастические, дискретные и непрерывные, линейные и нелинейные. И в каждом конкретном случае используются свои алгоритмы решения.
Отметим, что при изучении и оптимизации сложных объектов (систем) рассмотренные модели имеют ограниченное применение. Во-первых, они не учитывают, вообще говоря, противоречивых критериев (целевых функций), которые существуют в сложной системе. Во-вторых они не учитывают наличия иерархического (многоуровневого) строения реальных систем, в соответствии с которым каждый иерархический уровень может иметь свою совокупность критериев оптимизации. И, в-третьих, не учитывается неопределенность, обусловленная неполным знанием, неточностью и нечеткостью описаний системы управления, случайностью и конфликтностью ситуаций.
Многокритериальное управление. рассмотренные модели являются одноцелевыми и одноуровневыми моделями с детерминированной структурой. Основные же тенденции в формализации задач, как показывает анализ работ последних лет, состоят в построении и изучении многоцелевых, многоуровневых и расплывчатых (с недетерминированной структурой) моделей.
Ранее, когда приходилось сталкиваться с проблемой многокритернальности, часто все критерии, кроме одного, фиксировались и принимались в качестве ограничений, так что оптимизация проводилась по одному из них, который признавался доминирующим. Такая постановка вопроса, по сути дела, означала уход специалиста по системному анализу от решения задачи, и лицо, принимающее решение (ЛПР), оставалось один на один со сложной комбинированной проблемой многокритериального принятия решения.
Таким образом, в настоящее время возникла насущная потребность в более тонком подходе к многокритериальным проблемам, в использовании для этой цели аналитических методов. Модель многокритериальной оптимизации может быть записана в виде рассмотренных моделей с той разницей, что функции W(х) и W(х, u) являются векторными, т. е.
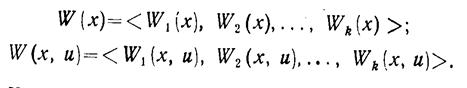
К настоящему времени как у нас, так и за рубежом накопился довольно обширный список литературы по многокритериальной (векторной) оптимизации. Существует несколько направлений исследования в области многокритериальной оптимизации.
Первое направление описывает различные способы с в е р т ы в а н и я многих целевых функций в одну. Этот подход наиболее старый и хорошо разработанный. Второе направление исследований связано с разработкой процедур, ориентированных не на решение четко поставленной математической задачи оптимизации, а на, последовательное выявление предпочтений Л П Р вместе с определением допустимого множества действий. Третий подход связан с рассмотрением методов так называемого м н о г о ц е л е в о г о п р ог р а м м и р о в а н и я для решения многокритериальных задач. В математическом отношении задачи, исследуемые в многоцелевом программировании, представляют собой задачи приближения вектор-функции, аргумент которой принадлежит некоторой допустимой области Х, к постоянному вектору (вектору целей). Приближение осуществляется путем минимизации расстояния в некоторой метрике между рассматриваемой вектор-функцией и постоянным вектором. При решении многокритериальных задач естественно считать компоненты вектор-функции как текущие значения критериев, а компоненты постоянного вектора – как желаемые значения этих критериев. Четвертое направление связано с разработкой функций полезности и теории игр.
Т е о р и я и г р. Теория игр представляет системы многоцелевых, но одноуровневых решений. Специфика этих многоцелевых систем заключается в том, что особое место среди условий, в которых приходится принимать решения, занимают условия конфликта. Здесь принимающему решение лицу (модели) приходится считаться не только со своими собственными целями, но также с теми целями, которые ставят перед собой другие участники игры (другие модели). Часто в качестве другого лица (другой модели) рассматривается природа (внешняя среда системы). Формальное описание теоретико-игровой системы состоит в следующем.
Пусть I – конечное множество, элементы которого называются и г р о к а м и (моделями), I= (1, 2,..., n). Г1оставим в соответствие каждому iÎI некоторое множество Хi, элементы которого назовем с т р а т е г и я м и (решениями) игрока i. Элементы декартового произведения Х= П Хi, т. е. х= (х1, х2,..., xn), называются с и т у а ц и я м и. Пусть, наконец, на множестве I´Х определена функция Wi(х), принимающая вещественные значения и называемая ф у н кц и е й в ы и г р ы ш а. Значение Wi(х) определяет выигрыш игрока i в ситуации х. Упорядоченная система
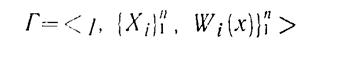
определяет игру в н о р м а л ь н о й ф о р м е. Содержание игры в нормальной форме состоит в том, что каждый из игроков, выбирая свою стратегию, участвует в создании ситуации, а когда ситуация создана, получает некоторый, зависящий от этой ситуации выигрыш. Естественно считать, что целью каждого игрока является достижение максимального значения своей функции выигрыша. Однако, так как выигрыш игрока зависит от ситуации х, а сам игрок может влиять на образование ситуации лишь частично, вопрос о том, как игрок может осуществить свою цель, оказывается нетривиальным. Ситуация, благоприятная для каждого из игроков, называется ситуацией равновесия игры. Понятие ситуации равновесия является центральным понятием теории игр.
Формальное определение игры, приведенное выше, оставляет весьма широкую свободу выбора конкретных возможностей для компонент, составляющих игру. Налагая на эти компоненты те или иные ограничения, можно получить различные классы игр. Собственно теория игр начинается тогда, когда множество 1 насчитывает не менее двух заинтересованных сторон. Следующим обобщением в теории игр является количество к о а л и ц и й д е й с т в и я. Каждая коалиция включает несколько игроков, объединивших свои стратегии. Если в игре имеется хотя бы одна коалиция действия К, то исследование игры становится содержательным.
Теория иерархического управления. Построение теории систем, обладающих иерархической структурой, одна из наиболее актуальных задач теории управления. Однако ее развитие встречает целый ряд трудностей принципиального характера. Оказывается, например, что анализ, а тем более синтез иерархических систем непосредственно не сводится к обычной теории оптимальных систем, так как каждое звено такой системы имеет возможность самостоятельно принимать решения.
Введение иерархической структуры связано с распределением между ее звеньями различных функций обработки информации и принятия решений. Однако децентрализация процесса управления служит источником новой неопределенности, которая проявляется в нетождественности интересов всей системы и ее отдельных звеньев. В связи с этим в теории иерархического управления возникают проблемы оптимальной централизации и децентрализации, оптимального распределения функций принятия решений между уровнями системы, оптимальной структуры, оптимальности в условиях многокритериальности и т. д.
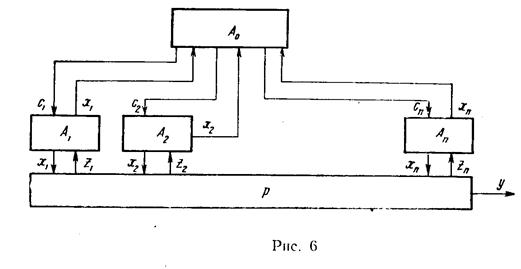
В самом общем виде структура иерархической системы управления представлена на рис. 6. Верхний уровень управления представлен блоком Аo, нижний уровень управления – блоками А1, А2,..., Аn. Производственный процесс определяется блоком Р. Соответственно модель управления верхнего уровня называется либо моделью центра, либо координирующей моделью, а модели управления нижнего уровня называются локальными.
Задача оптимизации в иерархической системе определяется в условиях, когда заданы критерии управления верхнего уровня Wo(c, х) и локальные критерии Wj(с, х), с= (с1,..., cn), х= (х1,..., хn). При этом параметры управления центра (координирующие параметры) и локальные параметры хj определяются областями допустимых значений, т. е. cÎC, хjÎХj. Представленное описание иерархической системы требует учета как вертикальных, так и горизонтальных связей управления.
Исходя из этого, общая модель управления иерархической системы может быть представлена следующим образом:
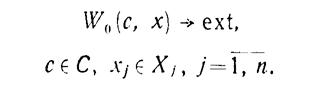
Пусть локальные модели системы имеют вид:
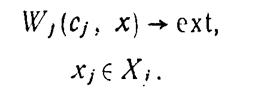
Это значит, что, кроме локального параметра управления хj, на значение критерия Wj имеют влияние и другие значения хi (i=l, 2,..., n, i¹j). Обозначим данную совокупность остальных значений {хi} через связующий параметр zj. Тогда локальная модель будет иметь вид:
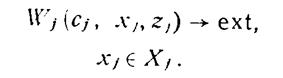
В этих условиях модель управления верхнего уровня может определяться следующим образом:
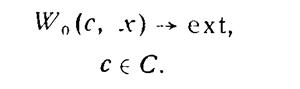
Учитывая обратные связи в иерархической структуре, можно итеративным образом обеспечить решение общей иерархической модели.
 2014-02-24
2014-02-24 3900
3900







