Сетевой метод

В настоящее время сетевой метод и связанное с ним сетевое планирование и управление широко распространены [4]. Этот метод применяют в самых различных отраслях народнохозяйственпой деятельности: при проектировании, подготовке и ремонте морских судов, при сооружении сложных производственных комплексов, в анализе информационных потоков и др.

**В основе сетевого метода лежит построение сетевой модели (сетевого графика), представляющей собой графическое изображение комплекса операций, реализация которых приводит к достижению поставленной цели.

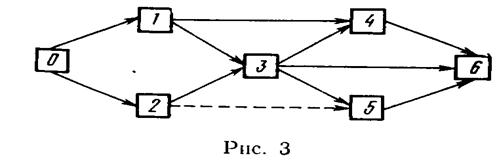
Первым шагом при составлении сетевой модели является расчленение данного комплекса на отдельные работы, в результате чего появляется перечень (список) работ. Одним из важнейших показателей для каждой работы является ее продолжительность. Следующий важный шаг в процессе составления сетевой модели – выявление всех технологических связей, которые существуют между отдельными работами и показывают последовательность выполнения работ. После выявления всех связей можно в перечне около каждой работы записать номера предшествующих ей работ. Факт начала (окончания) некоторой работы будем называть событием. Имея перечень работ, технологических связей и событий, можно составить сетевой график на языке работ и событий (рис. 3).

Здесь квадратом обозначено событие, прямой – работа. Пунктирная прямая изображает так называемую фиктивную работу, которая не связана ни с затратой времени, ни с затратой ресурсов.

Последовательность взаимосвязанных работ образует в сетевом графике так называемый путь m. Продолжительностью Тm пути m называют сумму продолжительностей тех работ, которые этот путь составляют. Путь, ведущий от начала сетевого графика к его концу и имеющий наибольшую продолжительность, называется критическим и обозначается m_кр, а его продолжительность называется критическим временем Tкр. Критическое время Ткр показывает наиболее ранний возможный срок выполнения того комплекса работ, который представлен данным сетевым графиком. Всякая задержка выполнения работы, лежащей на критическом пути, приводит к задержке выполнения работ всего комплекса. Это значит, что критический путь представляет собой «узкое место» в данном комплексе, поэтому он должен привлекать особое внимание руководства.

Существует несколько самых общих правил, относящихся к составлению и построению сетевого графика.

1. В сетевом графике не должно быть замкнутых контуров (циклов), т. е. путей, которые начинаются и заканчиваются в одном и том же событии.

2. В сетевом графике не должно быть работ, имеющих одинаковые коды, т. е. работ с одним и тем же предшествующим и последующим событием.

3. Все работы в сетевом графике должны быть простыми, что позволяет строго упорядочить последовательность их выполнения.

4.Если одно событие обязательно предшествует другому, то между ними вводится фиктивная работа.

Используя сетевые графики в целях выявления процессов, планирования и управления ими, прежде всего необходимо определить сроки свершения отдельных событий. При этом сроки следует отсчитывать от начального события, полагая срок свершения начального события равным нулю.

Следует различать возможные и допустимые сроки свершения событий. Рассмотрим сначала возможные сроки.

Для того чтобы какое-нибудь событие Аj свершилось, требуется, чтобы были закончены все работы (Ai1, Аj), (Аi2,Аj),..., (Аin,Аj), которые входят в это событие (рис. 4).

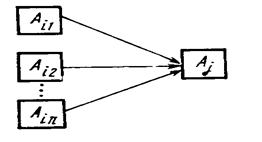
Рис.4

Обозначим множество работ, входящих в событие, через U_j⁺. Очевидно возможным сроком свершения j-го события Аj можно считать любой момент времени, который наступает после того, как выполнены все работы множества Uj+. Наиболее ранний из возможных срок свершения j-ro события является первым из основных временных параметров сетевого графика и обозначается через t_р(i).

Алгоритм вычисления t_p(j). Предположим, что для событий Аi1, Аi2,...,Аin (рис.3 и 4), которыми начинаются работы, входящие в j-e событие (работы множества Uj+), ранние сроки свершения уже вычислены, т. е. уже известны t_p(i1), t_p(i2),..., t_p(in). Тогда любой из возможных сроков свершения j-rо события t_вз(j)должен удовлетворять условию

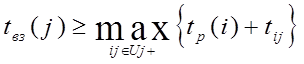
Следовательно, наиболее ранний из возможных сроков свершения j-ro события t_р(j) определяется следующим образом:

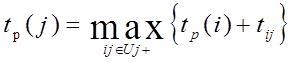
Таким образом, отправляясь от начального события, срок которого известен (t(0) =0), можно последовательно, по формуле расчета t_p(j), определить все ранние сроки свершения событий j сетевого графика. Ранний срок последнего события t_p(m) определяет критическое время свершения всего комплекса работ.

Теперь рассмотрим, какие же сроки свершения событий можно считать допустимыми. Дело в том, что при выполнении работ, которые лежат на путях, ведущих к j-му событию, могут произойти те дли иные задержки. В связи с этим j-е событие не наступит в минимально возможный срок t_p(j), и запаздает в сравнении с ним. Но слишком большое опоздание в сроке свершения j-го события может отразиться на сроке окончания всего комплекса работ. Очевидно, что допустимым сроком свершения события Аj можно считать такой срок, при котором «не сорвется» срок окончания всего комплекса работ, равный критическому времени Ткр. Наиболее поздний из допустимых срок свершения j-ro события является вторым из основных временных параметров сетевого графика и обозначается через t_п(j).

Алгоритм для вычислеиия t_п(j). Рассмотрим работы, исходящие из j-ro события, т. е. работы (Аj,Аk1), (Aj,Ak2,),..., (Аj,Аkq), (рис. 5).

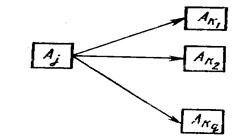
Рис.5.

Обозначим множество этих работ через Uj-. Допустим, что для всех событий Ak1, Аk2,,..., Аkq, которыми заканчиваются работы множества Uj-, уже вычислены наиболее поздние сроки их свершения, т. е. уже известны t_п(k1), t_п(k2),..., t_п(kq). Тогда допустимым сроком свершения j-ro события t_дп(j) может быть только такой срок, который, будучи сложен с продолжительностью любой работы множества Uj- (исходящей из j-ro события), даст момент времени, не превосходящий ни одного из сроков t_п(k1), t_п(k2),..., t_п(kq), т. е.

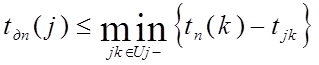
Следовательно, наиболее поздним из допустимых будет срок, определенный равенством

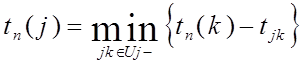
Таким образом отправляясь от конечного события, для которого t_п(m) =Tкр, можно по формуле расчета t_п(j) определить все поздние сроки свершения событий j сетевого графика.

Дальнейший анализ сетевых графиков связан с понятием резерва времени. Различают резервы времени пути, события и работы. Резервом времени пути m называется разность между критическим временем Ткр, и временной продолжительностью пути Тm он обозначается через Rm определяется следующим образом:

Rm = Tkp - Tm.

Очевидно, что для критического пути Rkp=0. Некритические пути имеют положительные резервы времени.

Резервом времени события Aj называется разность между наиболее поздним и наиболее ранним сроками свершения этого события. Обозначим резерв времени события Аj через Rj, тогда

Rj = t_п(j) - t_р(j)

Так как на критическом пути t_п(j) =t_р(j), то, следовательно, резервы времени для свершения событий на критическом пути равны нулю, т. е. Rj = 0.

Полным резервом времени работы (Ai,Aj), обозначаемым R_п(ij), называется величина, определяемая следующим образом:

R_п(ij) = t_п(j) -t_р(i) - tij

Полный резерв времени R_п(ij) для любой работы не отрицателен, R_п(ij) ³ 0, причем он равен нулю только тогда, когда работа (Аi,Аj) лежит на критическом пути. В дальнейшем такие работы будем называть критическими. Рассматривая какую-нибудь некритическую работу (Аi,Аj), можно по ее полному резерву R_п(ij) судить о том, каким запасом времени мы располагаем для увеличения продолжительности ее выполнения. Если резерв времени R_п=(ij) использован полностью, то такая работа и путь, который содержит эту работу, становятся критическими.

Примером использования сетевого метода может служить задача докового ремонта судна. Пусть для некоторого судна в доке должны быть выполнены следующие работы: 1) подготовительные, в том числе подготовка дока к приему судна, постановка судна в док и подключение сетей; 2) по якорному устройству, в том числе очистка якорных канатов, их освидетельствование, ремонт и окраска в цехах завода; очистка и окраска канатных ящиков; 3) по корпусу, в том числе очистка и освидетельствование корпуса, краска корпуса; 4) по группе – винт, дейдвуд, гребной вал, в том числе очистка, рихтовка, сварка и балансировка винта в цехах завода; проточка облицовок гребного вала, пригонка конуса винта; замена бакаута; 5) по рулевому устройству, в том числе очистка, ремонт и окраска пера руля; замена втулки нижней опоры; замена уплотнений баллера; очистка и окраска гельмпорта; 6) ремонт кингстонов, решеток и трубопроводов и их освидетельствование; 7) ремонт захлопок и отливных клапанов.

Этот список следует детализировать для того, чтобы можно было составить перечень работ. Далее следует выявить все связи между этими работами (технологические, логические, ожидания и т. д.). После этого можно приступать к составлению сетевого графика и расчетам его параметров.