Пример
Пример
Пример
Пример
Пример
Основные логические операции и таблицы истинности логических выражений
Вычитание большего числа из меньшего в двоичной системе
Чтобы из меньшего числа вычесть большее, необходимо:
1) вычесть из большего меньшее;
2) приписать к результату знак «минус».
Пример. Вычислить 11 - 111:
1) 111-11 = 100;
2) -100.
Умножение. Умножение в столбик двух двоичных чисел производится так же, как и с десятичными, последовательно умножая первое число (множимое) на очередную цифру второго числа (множителя). При этом правый разряд полученного числа записывается под той цифрой, на которую умножали. Затем результат складывается.
Таблица 3.5. Таблица умножения для двоичной системы счисления
| Пример х 11 +101 |
| х | = | |||
Деление. Многоразрядные числа делятся в столбик по тому же алгоритму, что и десятичные. Алгоритм для деления нацело:
1. Подбором найти число, которое при умножении на делитель дает число меньшее первых цифр делимого: 11 х 1 = 11. Записать это число в ответ.
|
|
|
2. Вычесть полученное произведение из первых цифр делимого и записать остаток. Приписать к нему следующую цифру делимого. Если полученное приписыванием число меньше делителя, то записать в ответ нуль и приписать следующую цифру делимого.
Повторять операции 1 и 2, пока не кончатся все цифры в делимом.
Таблица 3.6. Таблица деления
Пример
| : | = | -11 | ||||||
| -11 | ||||||||
| На ноль делить нельзя | 0 |
Сложное высказывание можно получить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности. Рассмотрим их подробней.
Операцией отрицания (инверсией) называют высказывание Ā (или ¬А, говорят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Присоединение «не» к высказыванию меняет его истинностное значение на противоположное. Отрицание – унарная (т.е. одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу «не».
Высказывание «Волга впадает в Каспийское море» – истинно, его отрицание «Неверно, что Волга впадает в Каспийское море» или «Волга не впадает в Каспийское море» – ложно. Наоборот, «Дважды два равно пять» — ложно, тогда «Неверно, что дважды два равно пять» или «Дважды два не равно пять» — истинно.
Это правило можно записать в виде соответствующей таблицы истинности (табл. 3.7).
Таблица 3.7. Таблица истинности для операции «отрицание»
(А – исходное высказывание, 1 – истина, 0 – ложь)
| А | Ā |
Таблица истинности логических выражений – таблица, в которой выписаны все сочетания истинностных значений исходных высказываний и истинностное значение сложного высказывания, полученного в результате применения логических операций.
|
|
|
Для основных логических операций по определению известно, при каких наборах значений исходных простых 
 высказываний сложное высказывание с этой связкой будет истинно. Исходя из этого, строятся таблицы истинности. Для сложных высказываний, в которых простые высказывания объединены несколькими связками, т. е. для построения которых использовались несколько логических операций, построение таблиц истинности помогает ответить на вопрос, при каких условиях сложное высказывание будет истинным, а при каких ложным.
высказываний сложное высказывание с этой связкой будет истинно. Исходя из этого, строятся таблицы истинности. Для сложных высказываний, в которых простые высказывания объединены несколькими связками, т. е. для построения которых использовались несколько логических операций, построение таблиц истинности помогает ответить на вопрос, при каких условиях сложное высказывание будет истинным, а при каких ложным.
Логическим умножением (конъюнкцией) двух высказываний А и В является новое высказывание С, которое истинно только тогда, кода истинны оба высказывания. Записывается С = А Ù В или С = А&В (при этом говорят С равно А и В).
Правило истинности для конъюнкции можно представить в виде табл. 3.8.
«2 = 2 и 3 = 3». Здесь истинно каждое из простых высказываний и, следовательно, истинно полученное высказывание. Иными словами: 1) истинно, что «два равно двум»; 2) истинно, что «три равно трем», следовательно, 3) истинно, что «два равно двум и три равно трем».
Таблица 3.8. Таблица истинности для операции «конъюнкция»
(А и В – исходные высказывания, 1 – истина, 0 – ложь):
| A | B | A & B |
Логическим сложением (дизъюнкцией) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = АÚВ или С = А + В (при этом говорят С равно А или В).
Таблица 3.9. Таблица истинности для операции «дизъюнкция»
(А и В – исходные высказывания, 1 – истина, 0 – ложь):
| A | B | A Ú B |
«2 = 2 или 2 = 5» – «два равно двум» истинно, «два равно пяти» ложно, высказывание «два равно двум или два равно пяти» – истинно.
Импликацией двух высказываний А (посылка) и В (заключение) является новое высказывание С, которое ложно тогда, когда посылка истинна, а заключение ложно. В остальных случаях импликация истинна.
Записывается С = А ® В или С = А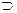 В (при этом говорят: из А следует В). Операция импликациипозволяет получить сложное высказывание из двух простых высказываний и грамматической конструкции «если..., то...».
В (при этом говорят: из А следует В). Операция импликациипозволяет получить сложное высказывание из двух простых высказываний и грамматической конструкции «если..., то...».
Такое сложное высказывание называют условное высказывание. Слово «то», можно заменить словом «следовательно». Часть импликации, идущая после слова «если», называется основанием, посылкой или антецедентом. Часть импликации, идущая после слова «то» называется следствием, заключением или консеквентом.
Таблица 3.10. Таблица истинности для операции «импликация»
(А и В – исходные высказывания, 1 – истина, 0 – ложь):
| A | B | A ® B |
Возьмем два высказывания «Сегодня идет дождь» и «На улице мокро». Построим сложное высказывание с импликацией: «Если сегодня идет дождь, то на улице мокро». Полученное сложное высказывание ложно, только если одновременно истинно «Сегодня идет дождь» и ложно «На улице мокро». Или, иными словами, когда истинны такие высказывания: «Сегодня идет дождь» и «На улице НЕ мокро». В остальных случаях сложное высказывание истинно. Когда истинны оба простых высказывания, истинно и сложное: «Сегодня идет дождь» – истинно, и «На улице мокро» – истинно, следовательно, «Если сегодня идет дождь, то на улице мокро» тоже – истинно. Сложнее понять, почему сложное высказывание с импликацией истинно, если ложна посылка (в нашем случае, когда ложно высказывание «Сегодня идет дождь»). На самом деле должно быть очевидно, что если «Сегодня НЕ идет дождь», то мы ничего не можем сказать о том, мокрые улицы или нет. Таким образом, из истины «Сегодня НЕ идет дождь» может следовать как «На улице мокро», так и «На улице не мокро».
|
|
|
Такой случай называется истинностьюв силу ложности посылки, или говорят, что из лжи может следовать все что угодно.
Эквиваленцией двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А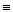 В или С = А
В или С = А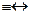 В. Полученное сложное высказывание содержит слова «если и только если», или «в том и только в том случае, когда», или «тогда и только тогда, когда». В общем виде такое высказывание выглядит так: «А, если и только если В». Оно получено из двух импликаций: «Если А, то В» и «Если В, то А». При этом говорят, что событие А равносильно событию В.
В. Полученное сложное высказывание содержит слова «если и только если», или «в том и только в том случае, когда», или «тогда и только тогда, когда». В общем виде такое высказывание выглядит так: «А, если и только если В». Оно получено из двух импликаций: «Если А, то В» и «Если В, то А». При этом говорят, что событие А равносильно событию В.
Эквивалентность истинна, если оба исходных высказывания имеют одинаковые истинностные значения. С ее помощью можно получить сложное высказывание из двух импликаций.
Таблица 3.11. Таблица истинности для операции «эквивалентность»
(А и В – исходные высказывания, 1 – истина, 0 – ложь):
| А | В | А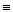 В В
|
«Треугольник является равносторонним тогда и только тогда, когда он является равноугольным». Если истинны оба высказывания «треугольник является равносторонним» и «треугольник является равноугольным», то полученное сложное высказывание истинно. Если оба простых высказывания ложны, т.е. истинны их отрицания «треугольник НЕ является равносторонним» и «треугольник НЕ является равноугольным», то полученное сложное высказывание «Треугольник НЕ является равносторонним тогда и только тогда, когда он НЕ является равноугольным» опять же истинно. В остальных случаях оно ложно.
С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения, которые называются булевыми функциями.
|
|
|
Таблица 3.12. Таблица истинности для операции (А®В) Ù (В®А),
где А и В — исходные высказывания, 1 — истина, 0 — ложь:
| А | В | А®В | В®А | (А®В) Ù (В®А) или А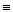 В В
|
Сначала, используя таблицу истинности для импликации, выписываем значения А ® В для каждой пары исходных значений А и В. Затем, аналогично, значения В ® А. Наконец, выписываем истинностные значения для конъюнкции (Ù), используя в качестве исходных значения двух предыдущих столбиков. Из полученной таблицы истинности видно, что данное сложное высказывание истинно, только если истинностные значения исходных высказываний совпадают, т. е. А и В или оба истинны, иди оба ложны. Такое отношение между А и В называется эквивалентностью.
 2014-02-24
2014-02-24 1916
1916
