Системы счисления принято делить на два класса: непозиционные и позиционные.
В непозиционных СС от положения (позиции) цифры в записи не зависит величина, которую она обозначает. Характерным примером такой системы счисления является римская СС.
Например, в римской СС число CCXXXII складывается из двух сотен, трех десятков и двух единиц и равно двумстам тридцати двум.
В римских числах цифры записываются слева направо в порядке убывания. В таком случае их значения складываются. Если же слева записана меньшая цифра, а справа – большая, то их значения вычитаются.
Например:
VI = 5 + 1 = 6, а IV = 5 – 1 = 4.
MCMXCVIII = 1000 + (-100 + 1000) + (-10 + 100) + 5 + 1 + 1 + 1 = 1998.
Такие системы счисления используются редко, т.к. не приспособлены для вычислений.
На практике наибольшее распространение получили позиционные системы счисления.
Позиционная система счисления – система счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр. В каждой позиционной системе счисления имеется основание. Любое число записывается в виде последовательности из цифр основания. Количество цифр основания равно самому основанию. Основание показывает, во сколько раз вес каждой цифры меньше веса цифры, стоящей в старшем соседнем разряде.
Некоторые позиционные системы счисления
Таблица 3.1
| Основание | Система счисления | Знаки |
| Двоичная | 0,1 | |
| Троичная | 0,1,2 | |
| Четвертичная | 0,1,2,3 | |
| Пятиричная | 0,1,2,3,4 | |
| Восьмиричная | 0,1,2,3,4,5,6,7 | |
| Десятиричная | 0,1,2,3,4,5,6,7,8,9 | |
| Двенадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В | |
| Шестнадцатиричная | 0,1,2,3,4,5,6,7,8,9,А,В,D,E,F |
Числа, которыми мы привыкли пользоваться, называются десятичными и арифметика, которой мы пользуемся, также называется десятичной. Называются они так потому, что каждое число можно составить из набора цифр содержащего 10 символов (цифр) –0123456789.
Возьмём, к примеру, число 246. Его запись означает, что в числе две сотни, четыре десятка и шесть единиц. Следовательно, можно записать следующее равенство:
246 = 200 + 40 + 6 = 2 * 102 + 4 * 101 + 6 * 100
Здесь знаками равенства отделены три способа записи одного и того же числа. Для нас наиболее интересна третья форма записи: 2 * 102 + 4 * 101 + 6 * 100. Она построена следующим образом:
В нашем числе три цифры. Старшая цифра "2" имеет номер 3. Так вот она умножается на 10 во второй степени. Следующая цифра "4" имеет порядковый номер 2 и умножается на 10 в первой степени. Уже видно, что цифры умножаются на десять в степени на единицу меньше порядкового номера цифры.
При этом пользуются следующим алгоритмом:
1) цифра в каждой позиции умножается на основание в степени на 1 меньшую, чем номер позиции;
2) полученные таким образом значения складываются.
Например:
12310 = 1 * 102 + 2 * 101 + 3 * 100;
1023.2810 = 1 * 103 + 0 * 102 + 2 * 101 + 3 * 100 + 2 * 10-1 + 8 * 10-2
В других системам счисления такой перевод будет выглядеть следующим образом:
1238 = 1х82 + 2 х 81 + 3 х 80 = 8310;
1012 = 1 х 22 + 0 х 21 + 1 х 20 = 510;
1Е316 = 1 х 162 + 14 х 161 + 3 х 160 = 48310.
Здесь индекс числа служит указанием на основание системы счисления. Назовем основанием системы счисления число, равное мощности множества (т.е. количеству элементов множества) различных символов, допустимых в каждой позиции числа.
Десятичная система счисления является однородной. Это означает, что одних и тех же символов достаточно для изображения любого числа. Но в повседневной жизни мы пользуемся и неоднородными системами счисления, и системами счисления с другим основанием. Пример тому – неметрические системы единиц (1 пуд=40 фунтов), система счета времени (1 минута = 60 секунд).
В дальнейшем мы будем рассматривать однородные позиционные системы счисления.
Обозначим через p основание системы счисления. Тогда веса позиций числа могут быть представлены следующим образом:
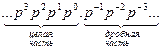
Таким образом, любое число X в позиционной системе счисления с основанием p можно представить в следующей развернутой форме записи:
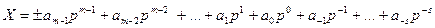 ,
,
или
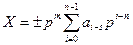 ,
,
где,
p – основание системы счисления;
m – количество позиций или разрядов, отведенное для изображения целой части числа;
s – количество разрядов, отведенное для изображения дробной части числа;
n = m + s – общее количество разрядов в числе,
ai – любой допустимый символ в разряде (т.е. должен принадлежать множеству {0,1, p-1}).
Заметим, что число, равное основанию системы счисления, в самой системе счисления записывается в виде:
pp=10p
В компьютерных науках наибольшее распространение получила не десятичная, а системы счисления с основанием, кратным 2 – двоичная, восьмеричная, шестнадцатеричная.
В двоичной системе счисления допустимыми символами являются только 0 и 1, а само число может быть представлено в виде последовательности нулей и единиц.
Например:
110100102 = 1 * 27 + 1 * 26 + 0 * 25 + 1 * 24 + 0 * 23 + 0 * 22 + 1 * 21 + 0 * 20 = 16210
В восьмеричной системе счисления допустимыми символами являются 0,1,…7.
Например:
2428 = 2 * 82 + 4 * 81 + 2 * 80 = 16210
В шестнадцатеричной системе допустимыми символами являются 0, 1, 9, A, B, C, D, E, F.
Например:
A216 = 10 * 161 + 2 * 160 = 16210
 2014-02-24
2014-02-24 41326
41326
