Комбинированный

Интервальный метод.

При использовании этого метода регистрации сигналов недостаток обнаруживается:

1. В задержке принятия информации на время .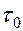

2. Если закон полной энергии за время 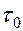будет равняться 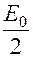, то тогда решение не определено.

Этот метод сочетает 2 предыдущих метода и позволяет избежать многих недостатков. Внутри значащего интервала 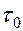стробирование. В этом случае при решении задачи 2 используется метод мажорирования. В этом случае импульсы должны быть частотными нечетными. Метод мажорирования совпадает с логической операцией неравнозначности (сложение по модулю 2).

Количественная мера информации.

Центральная проблема теории информации - это выбор меры информации. Будем рассматривать дискретный источник с четным множеством своих сочетаний.

Такой источник считается заданным, если задан ансамбль состоянии:

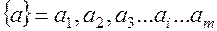
и обязательно должны быть заданы априорные вероятности этих состояний, каким способом мы их задаем не имеет значения):

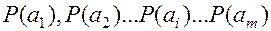, где 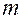- число возможных состоянии, 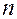- длина).

При 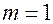- никакого выбора нет, источник находится в состоянии 1 (ничего нового не несет).
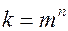- предложенная мера не обладает свойством аддитивности, т.е. не обладает свойствами линейно возрастать.

| Было замечено, что количество информации в сообщении вырабатывающего источника зависит от вероятности этого сообщения. Из соображения здравого смысла, менее вероятное событие несет больше количества информации.

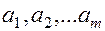события.

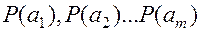- заданные вероятности.

Клод Шеннон вывел эту зависимость.

Если задан источник 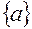, то 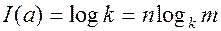- Хартли. Основание логарифма принципиальной меры не имеет:

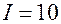, десятичная единица, (дит);

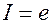, натуральная единица, (нат);

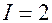, двоичная единица, (бит) - количество информации которое вырабатывает источник с двумя возможными состояниями.

К. Шеннон предложил оценивать количество информации содержащееся в сведе­нии о состоянии двоичного источника с равновероятными состояниями:

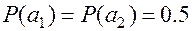
Было замечено, что количество информации в сообщении, вырабатываемом ис­точником, зависит от вероятности этого сообщения. Менее вероятное событие несет большее количество информации. Если имеется 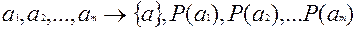тогда

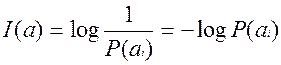
- эту зависимость вывел Клод Шеннон.

Пример: самая вероятная буква алфавита - "О", самая маловероятная - "Ф"

Для того, чтобы сравнить информационные свойства источника принято эту оценку проводить путем усреднения, т.е. провести операцию математического, ожидания.

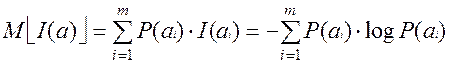это среднее количество информации на сообщение, которое вырабатывает источник. [^бит/_{сообщение} ]

Энтропия источника: 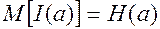- характеризует степень неопределен­ности состояния источника. (Но с точки зрения получателя информации: энтро­пия частично или полностью уменьшается).

Поскольку вычисленная таким образом энтропия не учитывает статистическую связь (корреляцию) между состоянием источника (сообщения), то такая энтропия называется безусловной (между сообщением 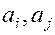нет корреляции).

Реально между состоянием источника существует статистическая связь (сущест­вует связь между состояниями ).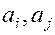

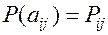- вероятность перехода из состояния 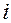в .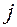

Для того, чтобы учесть статистическую связь, необходимо кроме априорных ве­роятностей 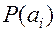знать переходные вероятности .

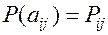Пример: задан источник с состоянием (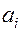) и априорные состояния .

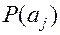Определить безусловную энтропию источника.

Ai	P(ai)
A1	0,5
A2	0,25
A3	0,125
A4	0,125

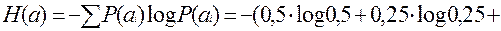
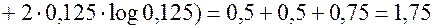
Хартли: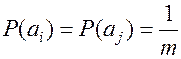

-это частный случай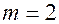

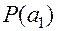- априорная вероятность состояния 1;

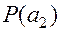- априорная вероятность состояния 2;

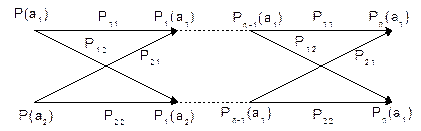
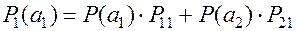
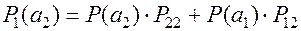
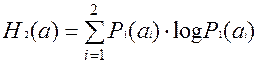
Удобной моделью источника с зависимыми выборами является Марковская модель. Представленный выше граф есть не что иное как модель однородного
марковского процесса с двумя состояниями.

Важной характеристикой Марковского процесса является его вектор финальных вероятностей за n - шагов перехода, т.е. за n - шагов перехода нужно найти эту матрицу (вектор):

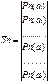
- матрица финальных состояний;

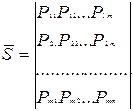
это полная группа несовместных событий, поэтому сумма коэффициентов по строке =1=>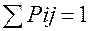

Необходимо знать вектор начальных вероятностей:

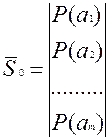
Вектор финальных вероятностей равен произведению матриц переходных веро­ятностей в степени n на вектор начальных вероятностей.

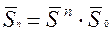
Пример: Задан двоичный источник информации (a₁,а₂), заданы априорные со­стояния (Р(а₁), P(a₂)) и переходная вероятность Pij.

Найти вероятность застать источник информации в состоянии а₁ и а₂ поcле п шагов перехода при условии, что процесс симметричный (т.е. переход из а₁ в а₁ равномерен с переходом а₂ и а₂).

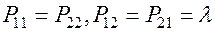() - симметричный процесс.

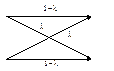
Составляем матрицу:

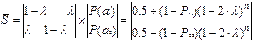
Из полученного выражения видно, что при 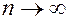финальные вероятности стре­мятся к 0,5, т.е. становятся равны.

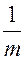
При этом -энтропия источника максимальная.

Энтропия.

Определяется но формуле:

;

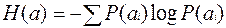где 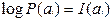- не статистическая случайная величина.

Свойства энтропии:

1. Максимальное значение энтропии - это когда все состояния источника равновероятны.

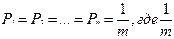- числе состояний источника.

Пример:

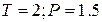
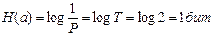
2. Энтропия равна нулю, если одно из состояний источника является достовер­ным событием, т.е. равна 1.

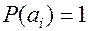
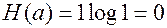
3. Энтропия всегда величина положительная (неотрицательная).

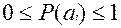
Это легко показать на графике:

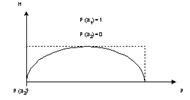
Значение ноль при 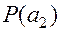- это следует из второго свойства энтропии.

Условная энтропия, определяемая через условные энтропии.

Задан источник с 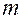состояниями:

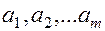— состояния

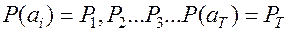— заданы априорные вероятности.

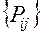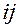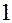(- это значит, что задаются интервалы – от до 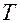, вероятность перехода из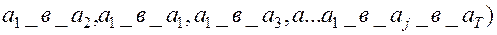

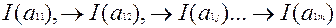- это случайные переходы.

Для того чтобы осуществить процесс перехода из одного состояния в другое, не­обходимо чтобы источник априори с вероятностью P(a_i) находился в состоянии ().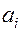

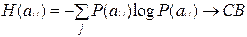
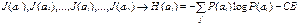
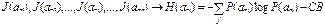
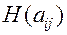- частная энтропия.

Эти все случайные величины - усредненные математические ожидания - к те­перь их необходимо еще раз усреднить:

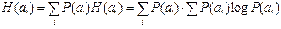- эту формулу первоначально вывел Клод Шеннон

Учет (наличие) статистической связи между источниками приводит к уменьшению энтропии (к степени неопределенности состояния источника).

Например: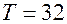

1 случай: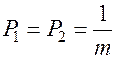

вероятность каждой буквы =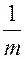

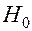- ничего не учитываем

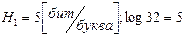
2 случай: если учтем неодинаковую вероятность, то

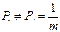, а статистическая связь не учитывается.

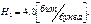(при условии, что вероятности неодинаковы).

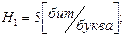
(8 - глубина учета статистической связи (глубина - 8 букв)).

Таким образом можно ввести понятие об избыточности сообщения (информации в сообщении; избыточности у источника не может быть).

формула избыточности

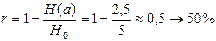
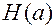- реальная энтрапия.

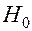- максимальная энтропия.

Производительность:

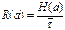
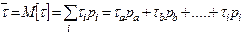
Математические модели сигналов, каналов и помех.

Сигналы, каналы и помехи являются объектами сложной природы. Например: сигнал представляется некоторой случайной функцией 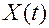X(t), канал задан своей функцией 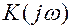со своим коэффициентом передачи и т.д.

Одной из идей позволяющих построить мат модель сигнала является разложение на элементарные сигналы.

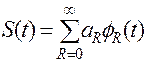
Появляется возможность решения некоторых задач по каналу K(t) в виде решения элементарных задач, которые заключаются в передаче простых функций (используя принцип суперпозиции).

K(t) {Bk(t)}

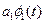
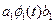
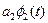
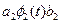
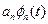
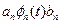
Если комбинация линейна и задача 4х-полюсник (канал) то на выходе получим линейную комбинацию.

Это будет справедливо лишь тогда, когда множество этих функций 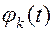-линейно независимы. (Линейные это когда жизнь каждой из элементарных функций независима, то есть время у них одинаково, но живут они в разных пространствах.)

Такими свойствами (линейной независимостью) обладает класс ортогональных функций.

Две ортогональные функции: .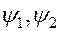

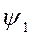
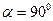
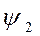
Свойства линейно независимых функций:

1. Математически это означает, что векторы элементарных функций взаимно перпендикулярны.

2. Любые два сигнала, выбранные из множества ортогональных, статистически независимы (не коррелированны).

Корреляция - статистическая связь.

Коэффициент корреляции определяется по следующей формуле:

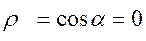
Общее условие: если две функции ортогональны, то:

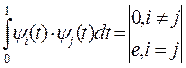
Интеграл характеризует взаимную энергию двух сигналов (но в нашем случае они линейно независимы и не имеют взаимной энергии).

Формула энергии сигнала :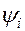

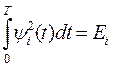
Средняя мощность процесса (средне статистическая мощность):

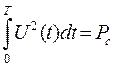
Иногда удобно чтобы 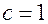,при 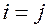. Для этого производят нормирование функций.

……,

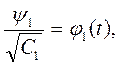
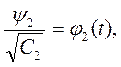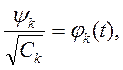
И тогда получим ортонормированны функции:

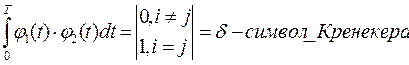
Примерами таких линейно независимых ортогональных функций являются функции Уолша, 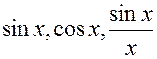и т.д.

Как вычислить весовой коэффициент?

Подставляем:

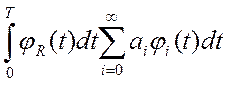
Учитывая свойство ортогональности, можно утверждать, что при всех 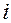-не равных 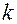этот интеграл равен нулю, и только водном случае,

Когда 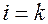, и будет равен интеграл :

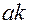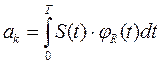-обобщенный коэффициент Фурье.

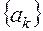-принято называть спектром колебаний (набор коэффициентов при разложении).

-если эти два сигнала ортогональны по энергии, то они ортогональны по мощности (но наоборот это условие выполняется необязательно).

Это выражение справедливо, когда число членов ряда бесконечно, в этом случае говорят, что энергия колеблется.

Энергия -это сумма элементарных энергий (то же самое и для мощностей).

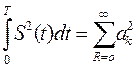
Функция задана на конечном интервале, а сумма энергий – на бесконечном интервале. Интересно, что на конечном интервале функция дает бесконечный спектр, а на бесконечном наоборот.

Выражение называется равенством Парсеваля. На практике ограничиваются конечным числом 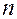, но тогда равенство не выполняется.

Можно попробовать среднеквадратическое:

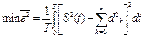
Для нашей дисциплины мы будем ограничиваться тремя функциями: 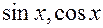. Таким образом получим разложение называемое, “ ряд Фурье”.

Если выбрать 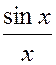, то получим ряд Котельникова, т.е. разложение по временным характеристикам.

В основе представления сигналов лежит ортогональное разложение.

Ортогональные это такие функции, которые не имеют взаимной энергии, мощности (они меняются во времени) и коэффициент корреляции которых равен нулю.