 Было установлено что любое сложное колебание можно представить суммой синусоид и косинусоид гармонически связанных друг с другом:
Было установлено что любое сложное колебание можно представить суммой синусоид и косинусоид гармонически связанных друг с другом:
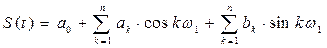
где 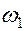 -круговая частота самого низкочастотного колебания которая связана с периодом этого колебания:
-круговая частота самого низкочастотного колебания которая связана с периодом этого колебания:
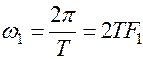 -первая гармоника.
-первая гармоника.
Все остальные гармоники пропорциональны первой 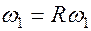 .
.
То тогда коэффициенты этого ряда рассчитываются следующим образом:
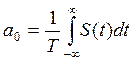
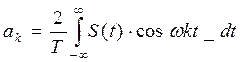

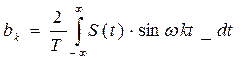
Подобного рода колебания  представляют собой ограниченный класс. Кроме того, функция
представляют собой ограниченный класс. Кроме того, функция  является периодической.
является периодической.
 теперь периодическая функция равная
теперь периодическая функция равная 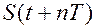 :
:
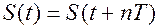
В 1807 году Фурье доказал что любую функцию  (даже такую которая имеет разрывы) можно представить в виде тригонометрического ряда, а коэффициенты рассчитываются также по формулам, интервалы интегрирования могут быть конечны.
(даже такую которая имеет разрывы) можно представить в виде тригонометрического ряда, а коэффициенты рассчитываются также по формулам, интервалы интегрирования могут быть конечны.
Для анализа этот конечный интервал разбивают на полуинтервалы 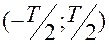 . Для периодических сигналов как видно из формулы (1) число гармоник равно бесконечности. Однако на практике число гармонических колебаний может быть ограничено. Дело в том что амплитуды
. Для периодических сигналов как видно из формулы (1) число гармоник равно бесконечности. Однако на практике число гармонических колебаний может быть ограничено. Дело в том что амплитуды 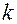 -тых гармоник убывают с ростом
-тых гармоник убывают с ростом 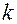 .
.
Среднеквадратическая погрешность:
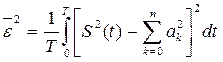
 2014-02-24
2014-02-24 368
368








