2014-02-24
559
Матрицы и простейшие операции над матрицами
Матрицей размера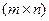 
называется упорядоченный массив чисел, состоящий из m строк и n столбцов.
В случае равенства строк и столбцов (m=n) матрица носит название квадратной матрицы (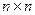
).
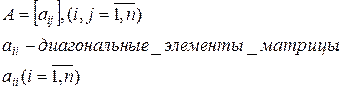
В случае, когда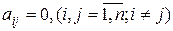 
, такая матрица называется диагональной.
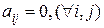- такая матрица называется нулевой.
Матрица размера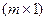 
называется вектор- столбец.
Матрица размера (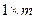
) называется вектор- строка.
Суммой матриц А+В= С является матрица С, элементы которой определяются по закону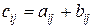 
.
Если в любой матрице строки и столбцы поменять местами, то получим транспонированную матрицу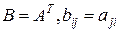 
.
При перемножении двух матриц С=А*В необходимо, чтобы количество столбцов матрицы А совпадало с количеством строк матрицы B (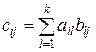
).
Свойства матричных операций:
.
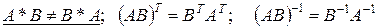Если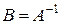 
, то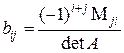 
,
где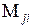 
- соответствующий минор матрицы 
.
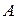Расчет матрицы податливости упругого элемента в новой базовой системе координат.
В зависимости от выбора системы координат (СК) матрицы податливости и жесткости будут изменять не только численные значения своих элементов, но и структуру.
Относительное положение любых двух прямоугольных систем координат характеризуется линейным смещением начал координат и угловым смещением осей координат.
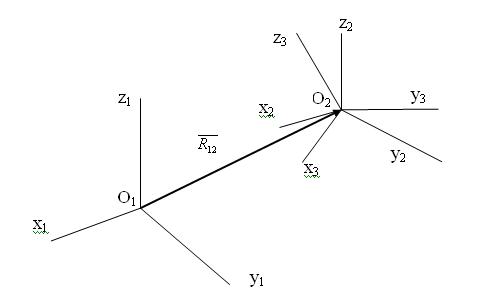
Рассмотрим переход из исходной СК (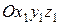
) в новую СК (
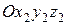) со смещенным началом координат:
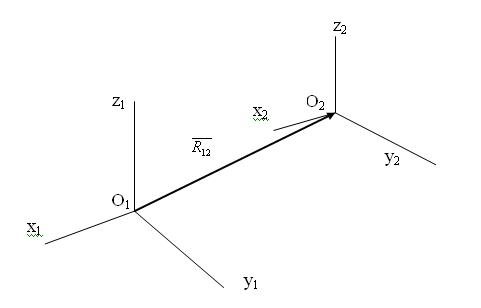
В матричной форме вектор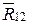 
имеет вид:
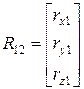
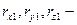проекции вектора на оси первой СК.
Отметим, что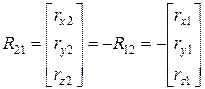 
.
Например, в данном рассматриваемом случае:
, 
.
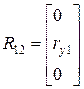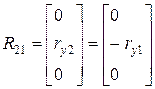Лекция 5.
Рассматривается общий случай относительного смещения начал координат двух СК (и ).
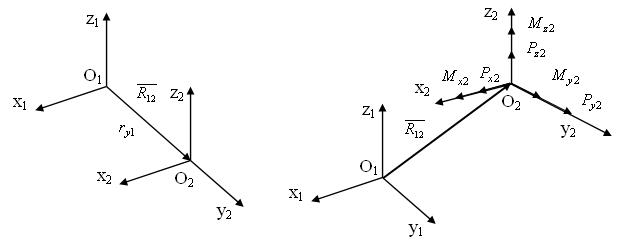
Поместим в нижнем индексе {i} номер системы координат, в которой матрица определяется, тогда уравнение равновесия будет иметь вид
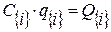. (5.1)
Здесь
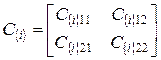- матрица жесткости (матрица коэффициентов из уравнения равновесия (5.1));
; 
.
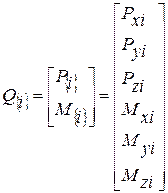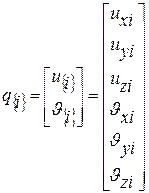При этом
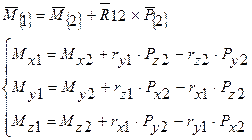( 5.2 )
Так как
;
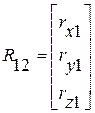то векторное выражение (5.2) можно записать в следующем матричном виде:
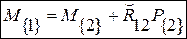; (5.3)
где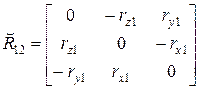 
- кососимметричная матрица;
.
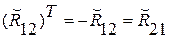Заметим далее, что
; 
; 
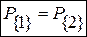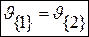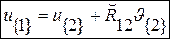. (5.4)
Распишем в блочном виде уравнение равновесия (5.1):
;
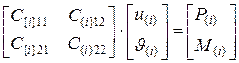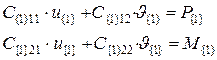(5.5)
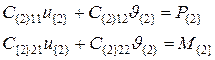(5.6)
Выражения (5.5), (5.6) – уравнения равновесия, записанные в первой и второй (исходной и последующей) системе координат.
Подставим выражения (5.3), (5.4) в уравнение равновесия (5.5):
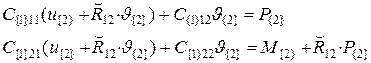
Приведем эти уравнения к стандартному виду.
Запишем сначала первое уравнение в виде:
.
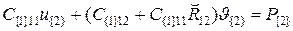Подставляем P{2} из первого уравнения в правую часть второго уравнения и переносим соответствующие слагаемые в левую часть второго уравнения:
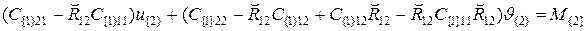. (5.7)
Сравнивая коэффициенты при обобщенных перемещениях в полученной системе (5.7) и в исходной системе (5.6), приходим к окончательным формулам расчета матрицы жесткости в новой системе координат со смещенным началом координат:
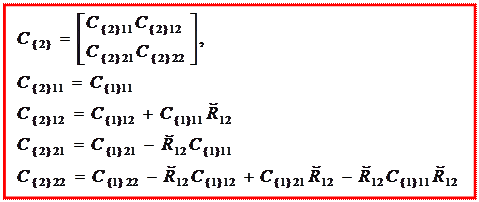
Аналогично получаем формулы для расчета матричных блоков матрицы податливости в случае смещения начала координат:
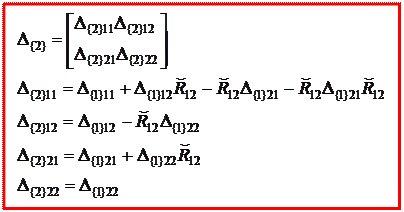
Лекция 6.
