Вернемся к выражению (1.4):
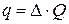 . (2.1)
. (2.1)
Умножим левую и правую части выражения (2.1) на 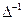
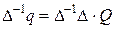 . (2.2)
. (2.2)
Тогда,обозначив 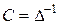 матрицу жесткости, получим уравнение равновесия в матричном виде
матрицу жесткости, получим уравнение равновесия в матричном виде
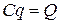 , (2.3)
, (2.3)
где 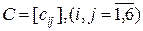 ;
; 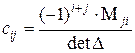 .
.
Здесь 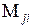 - минор матрицы
- минор матрицы 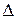 (определитель подматрицы, которая получается из данной матрицы
(определитель подматрицы, которая получается из данной матрицы 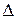 вычеркиванием
вычеркиванием 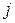 -ой строки и
-ой строки и 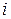 -го столбца).
-го столбца).
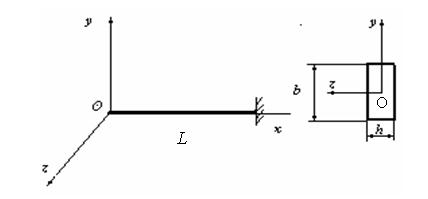
 Пример расчета матрицы податливости прямолинейного стержня:
Пример расчета матрицы податливости прямолинейного стержня:
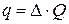 ;
;
где 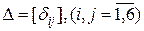 .
.
В рассматриваемом случае

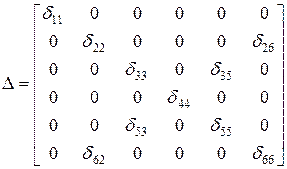
 .
.
1. Рассмотрим случай, когда i = 1.
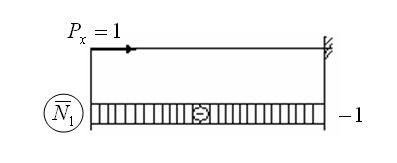
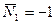
2. Рассмотрим случай, когда і = 2
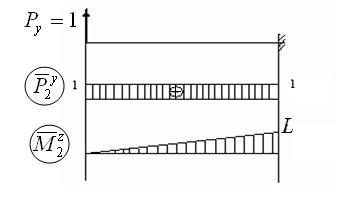
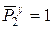
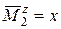
3.Расмотрим случай, когда і = 3:
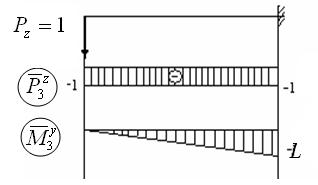
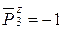 ;
; 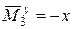 .
.
4.Рассмотрим случай, когда і = 4:
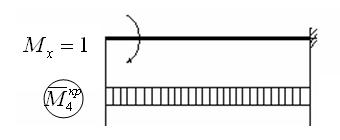
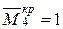 .
.
5.Рассмотрим случай, когда і = 5:
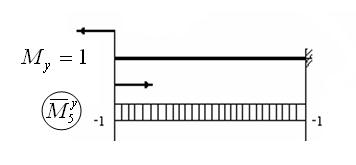
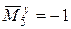
6. Рассмотрим случай, когда і = 6:
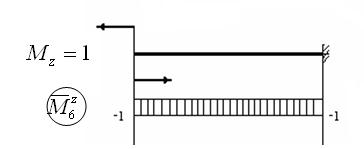
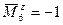
Тогда согласно формуле (1.6) получаем:
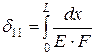 ;
; 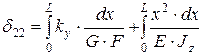 ;
; 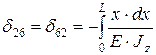 ;
;
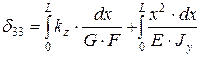 ;
; 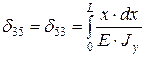 ;
;
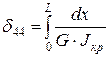 ;
; 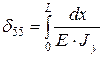 ;
; 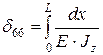 .
.
Рассмотрим матрицу податливости прямолинейного упругого элемента, имеющего переменное по длине сечение. Упругий элемент состоит из двух участков: М и Э.

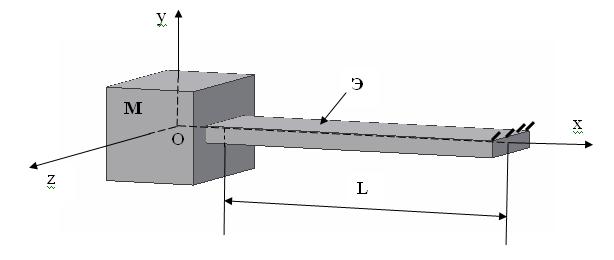
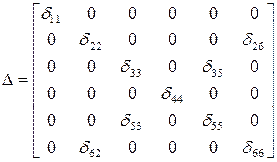
Рассматриваем матрицу податливости в системе координат Oxyz.
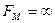 - площадь поперечного сечения инерционной массы;
- площадь поперечного сечения инерционной массы;
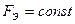 - площадь поперечного сечения упругого элемента;
- площадь поперечного сечения упругого элемента;
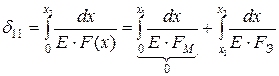 ;
;
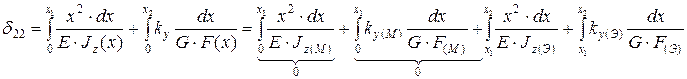 ;
;
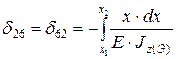 ;
; 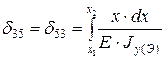 ;
;
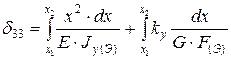 ;
; 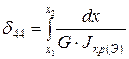 ;
; 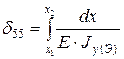 ;
; 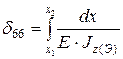 .
.
 2014-02-24
2014-02-24 741
741








