Задача о математическом маятнике.
Задача о физическом маятнике.
Задача о колебании груза на пружине.
Свободные гармонические колебания. Гармонический осциллятор.
Периодические колебания называются гармоническими, если они описываются законами sin или cos. Любая колеблющаяся система, любой физический процесс, описываемый законами sin или cos называется гармоническим осциллятором или просто осциллятором.
Примеры:
Дифференциальное уравнение свободных гармонических колебаний

Первоначально система находится в равновесии
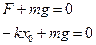
Систему вывели из положения равновесия на 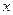 . Деформация будет
. Деформация будет  .
.
 | По второму закону Ньютона 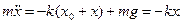 Преобразуем выражение к виду Преобразуем выражение к виду 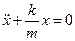 . Обозначим . Обозначим 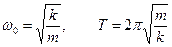 . Получим . Получим  . Это линейное однородное дифференциальное уравнение второго порядка. Оно описывает колебания . Это линейное однородное дифференциальное уравнение второго порядка. Оно описывает колебания |
груза на пружине. Решение его есть
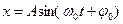 ,
,
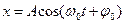 ,
,
что проверяется непосредственной подстановкой.
Физический маятник – это любое твердое тело, колеблющееся относительно оси, не проходящей через его центр.
Если ось проходит через центр тяжести, то тело находится в состоянии безразличного равновесия и колебаться не будет. Ось вращения проходит через точку О. Центр тяжести
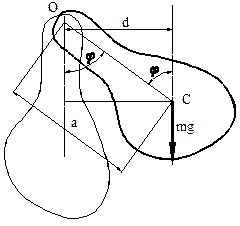 | Находится в точке С. ОС =а, 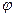 - угол поворота. В точке С приложена сила тяжести, в точке О – сила реакции, она направлена вертикально вверх. Поскольку она проходит через ось вращения, то ее момент равен нулю. Вращающий момент создает сила - угол поворота. В точке С приложена сила тяжести, в точке О – сила реакции, она направлена вертикально вверх. Поскольку она проходит через ось вращения, то ее момент равен нулю. Вращающий момент создает сила 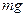 . . 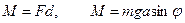 . Этот вращающий момент стремится вернуть тело к положению равновесия. . Этот вращающий момент стремится вернуть тело к положению равновесия. |
По второму закону Ньютона
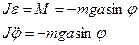
Знак (-) означает, что тело стремится в равновесие. Теперь
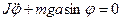 .
.
Это нелинейное дифференциальное уравнение, в него входит 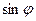 . Поэтому в общем случае физический маятник колеблется не по гармоническому закону. Рассмотрим частный случай, когда
. Поэтому в общем случае физический маятник колеблется не по гармоническому закону. Рассмотрим частный случай, когда 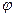 мало и
мало и 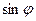 =
= 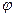 . Тогда
. Тогда
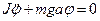 ,
, 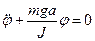 ,
,  ,
, 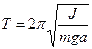 .
.
Уравнение
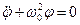
- это однородное линейное дифференциальное уравнение второго порядка. Оно описывает гармонические колебания.
Это частный случай физического маятника. Математическим маятником называется материальная точка, подвешенная на нерастяжимой нити. (Груз, подвешенный на нерастяжимой длинной нити, размерами груза по сравнению с длиной нити можно пренебречь):  - формула Гюйгенса.
- формула Гюйгенса.
При многих расчетах удобно представить формулу периода физического маятника как математического. Вводят приведенную длину физического маятника
 .
.
Тогда
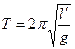 .
.
Приведенной длиной физического маятника называется длина такого маятника, период колебания которого равен периоду колебания данного физического маятника. Экспериментально, введя 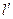 , определяют
, определяют 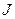 любого маятника. Подбирают длину математического маятника, чтобы
любого маятника. Подбирают длину математического маятника, чтобы 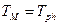 . Тогда
. Тогда  . Определяя
. Определяя 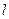 и
и 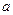 , находят
, находят 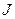 .
.
Продолжим рассмотрение гармонических колебаний.
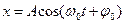
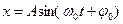
1) 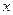 - смещение колеблющегося тела от положения равновесия в любой момент времени (или значение осциллирующего параметра в момент времени
- смещение колеблющегося тела от положения равновесия в любой момент времени (или значение осциллирующего параметра в момент времени 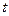 ).
).
2) 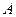 - амплитуда – максимальное отклонение от положения равновесия, или максимальное значение осциллирующего параметра,
- амплитуда – максимальное отклонение от положения равновесия, или максимальное значение осциллирующего параметра,  всегда.
всегда.
3)  - фаза колебания, измеряется в радианах, фаза определяет значение осциллирующего параметра в любой момент времени.
- фаза колебания, измеряется в радианах, фаза определяет значение осциллирующего параметра в любой момент времени. 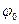 - начальная фаза в нулевой момент времени.
- начальная фаза в нулевой момент времени.
4) 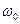 - собственная циклическая (круговая) частота.
- собственная циклическая (круговая) частота.
Связь 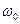 и
и 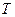 .
.
Рассмотрим значение осциллирующего параметра в моменты 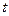 и
и  , где
, где 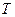 - период. По определению
- период. По определению 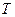 они должны быть одинаковы.
они должны быть одинаковы.
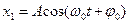 ,
,
 ,
,
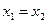
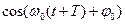 =
= 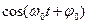 .
.
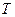 - наименьший промежуток времени, через который смещение повторилось. Поэтому аргументы
- наименьший промежуток времени, через который смещение повторилось. Поэтому аргументы  могут отличаться на
могут отличаться на 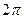 .
.
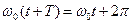 ,
, 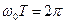 ,
,
 ,
,  ,
,  ,
,  ,
,
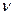 - число колебаний за 1 с,
- число колебаний за 1 с, 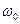 - число колебаний за
- число колебаний за 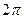 с.
с.
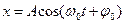
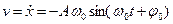 =
= 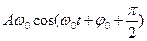
 - амплитудное значение скорости
- амплитудное значение скорости
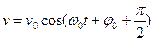
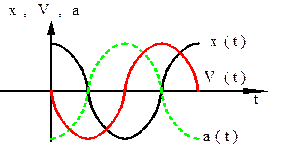
Скорость опережает смещение по фазе на 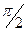 .
.
 =
= 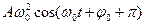
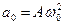
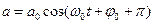
Сдвиг фаз между 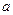 и
и 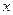 равен
равен 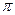 , они колеблются в противофазах.
, они колеблются в противофазах.
 2014-02-09
2014-02-09 1902
1902
