Ряды распределения СВ

Формула Бернулли (частная теорема о повторении опытов)

Пример 23

Имеется три лотерейных билета. Вероятность выигрыша для любого билета одинакова и равна р. Вероятность того, что билет не выиграет q = 1 – p – как вероятность противоположного события. Определить вероятность того, что из трех билетов выиграют ровно два.

Искомую вероятность обозначим .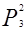

Интересующее нас событие произойдет, если выиграет первый И второй билет И не выиграет третий ИЛИ не выиграет первый билет И выиграют второй И третий ИЛИ не выиграет второй билет И выиграют первый И третий. Вероятность каждого из этих вариантов может быть найдена по формуле умножения, а ответ подсчитан по формуле сложения для несовместных событий:

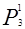= ppq + qpp + pqp = 3p²q.

Анализируя решение задачи, выясняем, что она была решена в следующем порядке:

- составлены различные варианты осуществления интересующего события;

- подсчитано количество этих вариантов;

- определена вероятность появления события, путём осуществления любого варианта;

- найдена искомая вероятность путём умножения вероятности появления события по одному из вариантов на общее количество вариантов.

Фактически, задача была решена по, так называемой, формуле Бернулли. Запишем ее в общем виде.

Пусть производится серия из n опытов (испытаний). Опыты проводятся неоднократно, независимо один от другого и в одинаковых условиях, так что вероятность появления события А от опыта к опыту не меняется и равняется р. Обозначим вероятность не появления события А в одном опыте- q = 1-p. Требуется определить вероятность того, что в серии из n опытов событие А повторится k раз – обозначим это событие как В.

Событие В может осуществиться различными способами (вариантами). Например, таким:

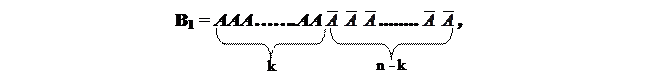или таким:

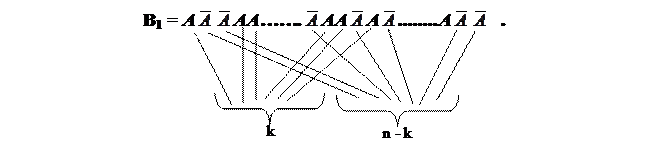Важно то, что в любом варианте количество появлений события А равно n, а количество появления события 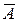равно n – k, хотя появляться и не появляться они будут в разных вариантах в различной последовательности.

Для определения числа подобных вариантов можно воспользоваться формулой комбинаторики - числом сочетаний из n элементов по k.

Сочетания – это такие комбинации из k объектов (элементов), выбранных из некоторого множества в n объектов, которые содержат одинаковое число объектов, но отличаются друг от друга хотя бы одним из них.

Число сочетаний из n элементов по k обозначается, как и может быть найдено по формуле: 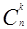= 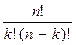. (15)

Важным свойством определения числа сочетаний является следующее:

= .

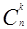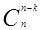В рассматриваемой задаче элементами, отличающимися друг от друга, являются номера опытов. Общее число вариантов равно .

Вероятность появления события А n раз для каждого варианта одинакова и может быть найдена по формуле умножения вероятностей исходя из фразы «Событие А произошло k раз и не произошло n – k раз»: p^kq^{n - k}

Суммируя эти одинаковые вероятности раз получаем формулу, называемую формулой Бернулли:

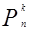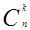=p^kq^n-k. (16)

Необходимо помнить, что р – это вероятность появления интересующего нас события в опыте, а q – вероятность непоявления этого события в опыте.

Формулу Бернулли.(Якоб Бернулли исследовал её в своей книге «Искусство предположений») также называют частной теоремой о повторении опытов. Это значит, что каждый последующий опыт проводится при тех же условиях, что и все предыдущие, т.е. вероятность появления события от опыта к опыту не меняется и остаётся равной р.

Наряду с частной существует общая теорема о повторении опытов (вероятность появления события от опыта к опыту меняется), рассмотрение которой выходит за рамки настоящего курса.

Пример 24

В цехе имеется 10 электродвигателей, вероятность отключенного состояния каждого из которых равна 0,1.Двишгатели включаются в сеть независимо один от другого. Определить вероятность того, что отключены сразу три электродвигателя.

Решение. Условие задачи соответствует схеме повторных испытаний Я. Бернулли. Решаем задачу с использованием частной теоремой о повторении опытов, учитывая, что отключенных двигателей три (вероятность отключенного состояния 0,1), а включенных – 7 (вероятность включенного состояния 0,9):

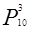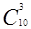=p³q^10-3 =[10!/3!(10-3)! ]q³(1-q)^10-3=120∙(0,1)³∙(0,9)⁷=0,0574.

Случайные величины и их законы распределения

Наряду со случайными событиями другим важнейшим понятием теории вероятностей является понятие «случайная величина» (СВ).

Величина – это количественная характеристика результата опыта.

Все величины делятся на две большие группы: неслучайные и случайные.

Неслучайные (детерминированные) – это такие величины, которые в результате опыта принимают заранее определенное, известное значение. Например, время восхода и захода солнца, дата наступления нового года, количество пальцев на руках у новорожденного, число экзаменов и зачётов в семестре.

Случайные(стохастические) – это такие величины, о которых заранее неизвестно, какое значение они примут в результате опыта.

Случайные величины, в свою очередь, могут быть дискретными и непрерывными.

Дискретными называют такие СВ, которые в опыте принимают какое-то одно из множества возможных значений, причем эти значения при желании можно перечислить или пронумеровать, т.е. это множество является конечным. Чаще всего (хотя не обязательно) - это целые, неотрицательные значения. Например, о ценка студента на экзамене; количество волос на голове, число работающих в цехе ЭД.

Непрерывными называют такие СВ, которые в опыте принимают какое-то одно из возможных значений, причем количество этих значений даже в очень малом интервале бесконечно велико. Иначе говоря, множество возможных значений непрерывной СВ является несчётным. Например, уровень напряжения в сети, длительность работы ЛЭП до отказа, рост и вес человека, масса авторучки.

Названия случайных величин принято обозначать заглавными буквами латинского алфавита – X, Y; а значения, которые случайные величины принимают в опыте, – строчными - x, y.

Различные значения одной и той же случайной величины наблюдаются не одинаково часто. Например, мужчины носят 42-й размер обуви гораздо чаще, чем 46-й; напряжение в сети гораздо чаще лежит в интервале 215- 225 В, чем в интервале 225 –235 В.

Взаимосвязь между значениями случайной величины и вероятностями их появления устанавливает з акон распределения случайной величины. Говорят, что СВ распределена (подчиняется) по тому или иному закону распределения. Существует несколько форм задания закона распределения:

· в виде таблицы (таблично);

· виде рисунка (графически);

· формулой (аналитически).

Способы задания законов распределения случайных величин

Все способы задания законов распределения СВ условно можно разделить на теоретические и статистические. Теоретические законы распределения отражают истинные законы, существующие в природе. Для их установления, согласно закону больших чисел, необходимо переработать близкий к бесконечному объём информации. Практически такие законы устанавливаются на основании ограниченного объёма статистических данных и оформляются теми или иными статистическими способами. Статистические данные часто называют экспериментальными (эмпирическими). Каждый теоретический способ задания закона распределения (ТЗР) имеет статистические аналогии (СтЗР). Рассмотрим эти способы.

ТЗР-1. Ряд распределения СВ

Ряд распределения – это таблица, в которой с одной стороны указаны значения случайной величины, а с другой – их вероятности (табл. 2). В ряду распределения значения СВ располагаются упорядочено – по мере их возрастания.

Между всеми возможными значениями СВ делится суммарная вероятность этих значений, равная единице. Поэтому сумма всех вероятностей ряда распределения равна единице: 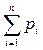= 1

Таблица 2. Ряд распределения СВ

Х	х1	х2	х3	…..	хi	…	хn
Р	р1	р2	р3	…..	рi	…	рn

Ряд распределения можно записать только в том случае, если СВ является дискретной, т.е. он является теоретическим способом задания закона распределения дискретной СВ.

Пример 25

Таблица 3. Ряд распределения экзаменационных оценок

Оценка
Р	0,10	0,45	0,30	0,15

СтЗР-1. Статистический ряд распределения

Статистический ряд является аналогией теоретического ряда распределения и устанавливает взаимосвязь между значениями СВ, полученными в опыте (их часто называют вариантами), и их статистическими вероятностями (частостями) - p_i*. Статистический ряд в целом называют также вариационным рядом.

Так как один и тот же объект может быть охарактеризован с разных сторон (например, для ЛЭП можно одновременно измерить ток, напряжение, активную и реактивную мощность, частоту и др.), то вариационные ряды могут быть одномерными, двумерными, трёхмерными и т.д. В дальнейшем будем рассматривать одномерные вариационные ряды.

В зависимости от того, как много вариант (значений СВ) х_i, получено эмпирическим путём статистические ряды подразделяются на негруппированные (безинтервальные) и группированные (интервальные).

СтЗР-1а. Негруппированный вариационный ряд

Этот ряд распределения (табл. 4) используется для описания статистических данных при малом (не более 15…20) числе k наблюдавшихся вариант.