Дисперсия случайной величины - характеристика разброса (рассеивания) значений случайной величины около центра распределения

Характеристик положения СВ недостаточно, для того, чтобы исчерпывающим образом судить об этой величине. Например, средняя заработная плата в России приближается к 15 тысячам рублей в месяц, но это не значит, что все жители живут хорошо. Стрелок может совершить несколько попаданий с большими отклонениями в разные стороны от центра мишени, что в итоге может дать среднюю координату попаданий близкую к центру мишени, что не свидетельствует о высоком мастерстве стрелка.

Наряду со средним значением СВ для суждения о распределении надо обязательно знать характеристику разброса (рассеивания) значений СВ около среднего. Среднее отклонение от центра распределения (первый центральный момент) такой характеристикой служить не может, так как из-за разных знаков отклонений всегда при усреднении даёт результат равный нулю. Необходимо каким-то образом «отстроиться» от знаков отклонений при их усреднении. Это можно сделать, определяя средние по модулю отклонения или возводя эти отклонения в квадрат. Именно последний способ и получил распространение.

Характеристика рассеивания - дисперсия – это второй центральный момент:

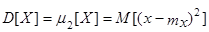. (31)

Для дискретной случайной величины: 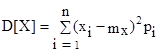. (32)

Для непрерывной случайной величины: 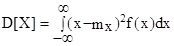. (33)

Свойства дисперсии:

1. Дисперсия – неслучайная величина, как и любой другой параметр закона распределения. По этой причине М[D_Х] = D_Х.

2. Статистической аналогией дисперсии является статистическая дисперсия.

Для негруппированного ряда: 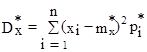; (34)

Для группированного ряда: 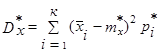. (35)

По закону больших чисел при неограниченном увеличении числа опытов статистическая дисперсия сколь угодно мало будет отличаться от теоретической.

3. Для практических расчётов нахождение дисперсии как второго центрального момента не очень удобно из-за громоздкости расчётов. Рекомендуется проводить расчёты по формулам, устанавливающим связь дисперсии с начальными моментами:

D_Х = α₂(х) – m_Х²; D_Х^* = α₂^*(х) – m_Х^*2. (36)

Эти формулы получены следующим образом: 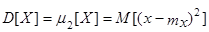= М[х² + 2хm_Х + m_Х²] = М[х²] - М[2хm_Х] + М[m_Х²] = α₂(х) - 2m_Хm_Х + m_Х² = α₂(х) – m_Х².

4. Дисперсия принимает любые неотрицательные значения.

5. Размерность дисперсии равна квадрату размерности случайной величины.

Это свойство дисперсии делает ее неудобным для применения вследствие непривычности получающейся размерности. Например, дисперсия напряжения измеряется в квадратных вольтах, а дисперсия тока в А² и т.д. По этой причине для характеристики рассеивания часто используют среднее квадратическое отклонение (СКО).

6. Среднее квадратическое отклонение σ_Х является квадратным корнем из дисперсии: . (37)

Размерность СКО совпадает с размерностью СВ.

7. Дисперсия неслучайной величины С равна нулю:

D [C] = М[(С – М(С))²] = М[(С – С)²] = М[0] = 0.

8. Неслучайную величину С можно выносить за знак дисперсии, возводя её в квадрат: D[CX] = С²D[Х].

Доказательство: D[CX] = М[(СХ – М(СХ))²] = М[(CХ – СМ(Х))²] = М[С²(Х – М(Х))²] = С²М[(Х – М(Х))²] = С²D[Х].

Пример 32. D[-3X] = 9D[X])

9. Дисперсия суммы независимых СВ равна сумме дисперсий этих величин:

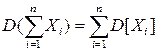. (38)

Доказательство проведём на примере двух дискретных СВ Х и Y (табл.11).

D[X+Y] = М[(Х + Y)²] – (М[Х + Y])² = М[(Х² + 2ХY + Y²)] – (М[Х] + М[Y])² =

= М[Х²] + М[2ХY] + М[Y²] – (М[Х]² + 2 М[Х] М[Y] + М[Y]²) =

= М[Х²] + 2М[Х]М[Y] + М[Y²] – М[Х]² - 2 М[Х] М[Y] - М[Y]²) =

= М[Х²] – М[Х]² + М[Y²] - М[Y]²) = D[X]+D[Y].

При большем числе слагаемых это свойство можно обосновать, используя приём, применённый для 7-го свойства МО.

Следствие 1. Дисперсия разности независимых СВ равна сумме дисперсий: D[X – Y] = D[X] + D[-Y] = D[X] + (-1)²D[Y] = D[X] + D[Y].

Следствие 2: Дисперсия суммы случайной и неслучайной величин равна дисперсии случайной величины: D[X+C] = D[X] + D[C] = D[X].

Так как суммирование неслучайной и случайной величин равноценно сдвигу начала координат в новую точку, можно заключить: дисперсия СВ не зависит от выбора начала координат.

10. Дисперсия произведения независимых СВ определяется выражениями:

- для двух СВ: D[XY] = М[(ХY)²] – М[ХY]² = М(Х²Y²) – (М[Х]М[Y])² =

= М[Х²]М[Y²] – (М[Х]²М[Y]² = (D[Х] + m_Х²) (D[Y] + m_Y²) - m_Х² m_Y² =

= D[Х] D[Y] + m_Х²D[Y] + m_Y²D[Х].

- для n независимых случайных величин:

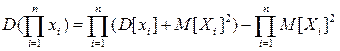. (39)

Пример 33. Определить дисперсию 3Х – 2Y – 4, если D[Х] = 5, D[y] = 6.

Решение:D[3Х – 2Y + 4] = D[3X] + D[-2Y] + D[4] = 9D[X] + 4D[Y] = 9·5 + 4·6 = 69.

Характеристики «скошенности» и «островершинности» закона распределения случайных величин

Третий центральный момент служит для характеристики асимметрии «скошенности» распределения. Он имеет размерность куба случайной величины; чтобы получить безразмерную характеристику и «отстроиться» от одновременной оценки разброса третий момент делят на куб среднего квадратического отклонения. Полученная величина называется коэффициентом «скошенности»:.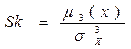

При положительной асимметрии (рис. 51) более пологая и длинная часть кривой распределения располагается справа от математического ожидания, а при отрицательной (рис. 52) – слева.

Четвертый центральный момент служит для характеристики островершинности и плосковершинности кривой распределения. Эти свойства описываются с помощью коэффициента эксцесса: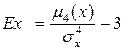

Для нормального закона распределения (закона Гаусса) Ех = 0.

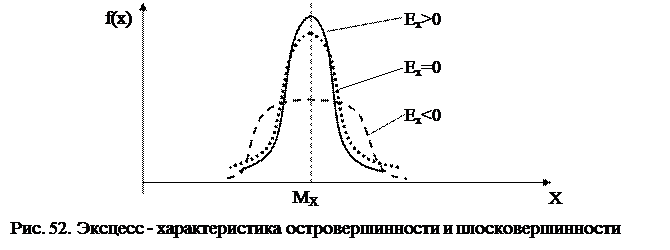Кривые, островершинные по сравнению с нормальным законом распределения, обладают положительным эксцессом, плосковершинные – отрицательным (рис. 52).