2014-02-24
550
Пусть r задано на множестве X, r Í Х2.
1. Рефлексивность: " х Î Х х r х.
Отношение r на множестве X называется рефлексивным, если для любого хÎХ имеет место х r х, то есть каждый элемент находится в отношении r к самому себе.
Матрица рефлексивного отношения имеет единичную главную диагональ, а граф – петлю возле каждого своего элемента.
2. Антирефлексивность: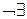 
х Î Х х r х.
Отношение r на множестве X называется антирефлексивным, если не существует хÎХ такого, чтоимеет место х r х, то есть ни один элемент не находится в отношении r к самому себе.
Матрица антирефлексивного отношения имеет нулевую главную диагональ,а граф – не имеет ни одной петли.
3. Нерефлексивность: $ х Î Х (x, x) Ï r.
4. Симметричность: " х, y Î Х х r y => y r х.
Отношение r на множестве X называется cимметричным, если для всех х и y из Х, из принадлежности (x,y) отношению r следует, что и (y,x) принадлежит отношению r.
Матрица симметричного отношения симметрична относительно главной диагонали, а граф – для каждой дуги (x,y) существует обратная дуга (y,x).
|
|
|
5. Антисимметричность: " х, y Î Х х r y, y r х Û x = y.
Отношение r на множестве X называется антиcимметричным, если для всех х и y из Х, из принадлежности (x,y) и (y,x) отношению r следует, что x=y.
Матрица антисимметричного отношения не имеет ни одной симметричной единицы относительно главной диагонали, а граф – для каждой дуги (x,y) не существует обратная дуга (y,x) и наоборот.
Свойства симметричности и антисимметричности не являются взаимоисключающими, примером может служить отношения равенства на множестве натуральных чисел.
6. Транзитивность: " х, y, z Î Х х r y, y r z => x r z.
Отношение r на множестве X называется транзитивным, если для всех х,y,z из Х, из принадлежности (x,y) и (y,z) отношению r следует, что (x,z) также принадлежит r.
Отношение r на множестве X называется антитранзитивным, если для всех х,y,z из Х, из принадлежности (x,y) и (y,z) отношению r не следует, что (x,z) также принадлежит r.
Отношение порядка – антисимметрично, транзитивно.
Отношение нестрого порядка (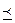
) - рефлексивно,
антисимметрично,
транзитивно.
r= { (x, y) | x³y, x,y Î N},
r= { (x, y) | x£y, x,y Î N}.
На множестве множеств: “A Í B”, “A=B”.
Отношение строгого порядка (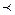
) - антирефлексивно,
антисимметрично,
транзитивно.
r= { (x, y) | x>y, x,y Î N},
r= { (x, y) | x<y, x,y Î N}.
На множестве множеств: “A Ì B”.
В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.
Отношения полного порядка:
r= { (x, y) | x³y, x,y Î N },
r= { (x, y) | x£y, x,y Î N }.
Отношения частичного порядка:
r= { (x, y) | x>y, x,y Î N },
|
|
|
r= { (x, y) | x<y, x,y Î N },
на множестве множеств: “A Í B”, “A Ì B”.
