Понятие о моментах случайной величины

Кроме перечисленных ранее параметров случайной величины в теории вероятностей используется ещё ряд характеристик, каждая из которых описывает то или иное свойство распределения. В качестве таких характеристик чаще всего применяют так называемые моменты.

Понятие момента широко применяется в механике для описания распределения масс (статические моменты, моменты инерции и т.д.). Совершенно теми же приёмами пользуются в теории вероятностей для описания основных свойств распределения случайной величины. Чаще всего применяются на практике моменты двух видов: начальные и центральные.

Начальным моментом s-го порядка д.с.в. Х называется сумма вида:

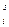_s[X] = xp_i.

Для н.с.в. Х начальным моментом s- го порядка называется интеграл

_s[X] = 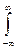x²f(x)dx.

Нетрудно убедиться, что основная характеристика положения- математическое ожидание - представляет собой не что иное, как первый начальный момент случайной величины Х.

Пользуясь знаком математического ожидания, можно написать общую формулу начального момента s-го порядка, справедливую как для д.с.в., так и для н.с.в:

_s[X] = M[X^s],

Иначе говоря, начальным моментом s-го порядка случайной величины Х называется математическое ожидание s- ой степени этой случайной величины.

Введем новое понятие «центрированной случайной величины».

Пусть имеется случайная величина Х с математическим ожиданием m_x (такое обозначение математического ожидания часто используется наряду с M(X)).

Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от ее математического ожидания:

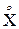= Х - m_x

Нетрудно убедиться, что математическое ожидание центрированной случайной величины равно нулю, так как:

M[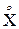] = M[X- m_x] = (x_i – m_x)p_i = x_i p_i - m_xp_i = =m_x – m_x = 0.

Аналогично и для н.с.в.