Числовые характеристики случайной величины

Каждый закон распределения представляет собой некоторую функцию, и указание этой функции полностью описывает случайную величину с вероятностной точки зрения. Однако, во многих вопросах практики нет необходимости характеризовать случайную величину полностью, исчерпывающим образом. Часто достаточно бывает указать только отдельные числовые параметры до некоторой степени характеризующие существенные черты распределения случайной величины. Такие характеристики, назначение которых - выразить в сжатой форме наиболее существенные особенности распределения, называются числовыми характеристиками случайной величины.

Среди числовых характеристик случайной величины нужно прежде всего отметить те, которые характеризуют положение случайной величины на числовой оси, т.е. указывают некоторое среднее, ориентировочное значение, около которого группируются все возможные значения случайной величины.

Из характеристик положения важнейшую роль в теории вероятностей играет математическое ожидание случайной величины, которое иногда называют теоретическим средним значением.

Рассмотрим д.с.в. Х, имеющую возможные значения х₁, х₂, …, х_n с вероятностями p₁, p₂, …, p_n.

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений. Если рассматривать x₁, x₂, …, x_n как координаты точек, лежащих вдоль некоторого стержня, а p₁, p₂, …, p_n - как веса грузов, подвешенных в этих точках, то M(x) будет совпадать с координатой центра тяжести образовавшейся системы.

0 х х М(х) х Х

p₁ p₂ p_n

Пример. Определить математическое ожидание выпадаемого числа очков при бросании игральной кости.

Решение. Составим ряд распределения.

M(x) = 1/6(1+2+3+4+5+6) = 3,5.

Для н.с.в. математическое ожидание выражается не суммой, а интегралом:

M(x) = 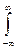xf(x)d(x)

Пример. Случайная величина подчинена закону распределения, плотность которого:

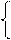2x при 0 < x < 1;

f(x) =

0 при x < 0; x >1;

Математическое ожидание случайной величины X:

M(x) = 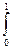xf(x)dx = 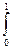2x²dx = 2/3

Кроме математического ожидания на практике иногда применяются и другие характеристики положения, в частности, мода и медиана случайной величины.