 f(x) P(x)
f(x) P(x)
 | |||
 |

Mo(x) X Mo(x) Х
Если многоугольник распределения (кривая распределения) имеет больше одного максимума, распределение называется "полимодальным". Иногда встречаются распределения, обладающие посредине не максимумом, а минимумом. Такие распределения называют "антимодальными". В общем случае мода и математическое ожидание не совпадают.
Часто применяется и еще одна характеристика положения - так называемая медиана случайной величины. Этой характеристикой обычно пользуются для н.с.в., хотя формально ее можно определить и для д.с.в.
Медианой случайной величины Х называется такое ее значение Ме(х), удовлетворяющее условию: интеграл плотности вероятностей (сумма вероятностей) значений х, меньших Ме(х) равен интегралу плотности вероятностей (сумме вероятностей) значений х, больших Ме(х), т.е. для н.с.в.:
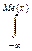 f(x)dx =
f(x)dx = 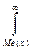 f(x)dx = 1/2.
f(x)dx = 1/2.
Геометрически медиана - это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
 |
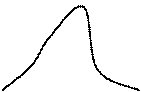

 f(x) S1= S 2= 1/2
f(x) S1= S 2= 1/2
 |




 |
Me(x) X
M(x), Mo(x), Me(x) - это характеристики положения.
Кроме характеристик положения - средних, типичных значений случайной величины, существуют еще характеристики рассеивания.
Основной числовой характеристикой рассеивания одномерной случайной величины X является дисперсия D(x).
Дисперсия – это сумма произведений квадратов отклонений случайной величины Х от ее математического ожидания на соответствующие вероятности.
Для д.с.в.: D(x) = 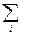 [xi – M(x)]2p(xi) =
[xi – M(x)]2p(xi) = 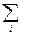 x
x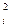 p(xi)- [M(x)]2;
p(xi)- [M(x)]2;
для н.с.в.: D(x) = 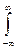 [xi- M(x)]2f(x)dx =
[xi- M(x)]2f(x)dx = 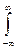 x2f(x)d(x)- [M(x)]2.
x2f(x)d(x)- [M(x)]2.
Весьма часто вместо дисперсии пользуются другой характеристикой, непосредственно с ней связанной, а именно, теоретическим средним квадратическим отклонением (или стандартным отклонением) 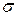 х:
х:
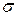 х=
х= 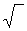 D(x);
D(x);
Удобство пользования средним квадратическим отклонением в качестве меры рассеивания вместо D(x) заключается в том, что оно выражается в тех же единицах измерения, что и сама величина X, тогда как дисперсия выражается в квадратах соответствующей единицы измерения.
Пример. Вычислить дисперсию D(x) и среднее квадратическое отклонение 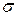 x по следующим данным:
x по следующим данным:
| Xi | X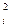
| P(xi) | XiP(xi) | Xi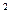 P(xi) P(xi)
|
| 1/32 | ||||
| 5/32 | 5/32 | 5/32 | ||
| 10/32 | 20/32 | 40/32 | ||
| 10/32 | 30/32 | 90/32 | ||
| 5/32 | 20/32 | 80/32 | ||
| 1/32 | 5/32 | 25/32 | ||
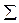
| 2,5 | 240/32 |
D(x) = 240/32 – 2,52 = 1,25; 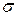 (x) =
(x) = 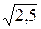 = 1,12.
= 1,12.
Пример. Функция распределения случайной величины X задана графиком. Найти M(x) и D(x).
 |
F(x)



 1
1
 a b X
a b X
Составим уравнение:
(x2 – x1)/(x2 – x1) = (y – y1/(y2 – y1);
(x – a) /(b – a) = y;
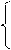 0 при x < a; F(x)= (x – a)/ (b – a) при а < x
0 при x < a; F(x)= (x – a)/ (b – a) при а < x 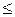 b;
b;
1 при x > b;
f(x) = FI (x) = 1/(b – a); M(x) = 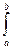 [x/(b – a)] dx = x2/2(b – a)|
[x/(b – a)] dx = x2/2(b – a)| = (b + a)/2; D(x) =
= (b + a)/2; D(x) = 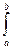 [x2/(b – a)]dx – [(b + a)/2]2 = x3/3(b – a)|
[x2/(b – a)]dx – [(b + a)/2]2 = x3/3(b – a)| =
=
= [(b3 – a3)/3(b – a)] – (a + b)2/4 = (a – b)2/4.
Пример. Выражение плотности распределения имеет вид:
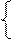 |
f(x) = 2x при 0 < x < 1;
0 при x < 0, x > a;
Найти дисперсию.
D(x) = 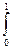 x2f(x)dx – [M(x)]2, M(x) = 2/3 (см. пример на стр.)
x2f(x)dx – [M(x)]2, M(x) = 2/3 (см. пример на стр.)
D(x) = 2x4| - [2/3]2 = (1 /2) - (2/3)2 = 1/18.
- [2/3]2 = (1 /2) - (2/3)2 = 1/18.
Пример. Найти математическое ожидание и дисперсию для случайной величины, подчиняющейся закону распределения Пуассона:
P(m) = (am/m!)ea, m = 0, 1, …,
a – некоторая положительная величина, называемая параметром Пуассона.
M(x) = 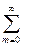 mP(m) =
mP(m) = 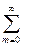 (mam/m!)e-a,
(mam/m!)e-a,
при m = 1 первый член суммы равен единице.
M(x) = 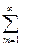 (mam/m!)e-a = a e-a
(mam/m!)e-a = a e-a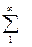 am-1/(m-1)! = a e-aea = a,
am-1/(m-1)! = a e-aea = a,
D(x) = 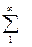 [(m2am)/m!]e-a – a2, D(x) = a
[(m2am)/m!]e-a – a2, D(x) = a 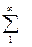 [mam-1/(m-1)!]e-a – a2,
[mam-1/(m-1)!]e-a – a2,
D(x) = a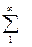 {[(m – 1) + 1]am-1/(m-1)!}e-a – a2 = aa +a – a2.
{[(m – 1) + 1]am-1/(m-1)!}e-a – a2 = aa +a – a2.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию.
 2014-02-24
2014-02-24 1813
1813
