Пусть имеется непрерывная величина Х с функцией распределения F (x), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность попадания этой случайной величины на участок от х до х +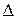 х:
х:
P (x < X < x + 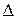 x <) = F (x +
x <) = F (x + 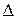 x) – F (x),
x) – F (x),
т.е. приращение функции распределения на этом участке. Рассмотрим отношение этой вероятности к длине участка, т.е. среднюю вероятность, приходящуюся на единицу длины на этом участке и будем приближать 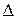 x к нулю. В пределе получим производную от функции распределения:
x к нулю. В пределе получим производную от функции распределения:

 lim F (x +
lim F (x + 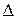 x) – F (x)/
x) – F (x)/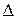 x = F/ (x) = f (x)
x = F/ (x) = f (x)
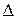 x
x 0
0 





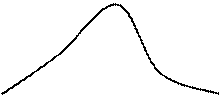
Функция f (x) - производная функции распределения - характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе "плотностью вероятности") непрерывной случайной величины X. Иногда функцию f (x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения. Плотность распределения, также как и функция распределения, есть одна из форм закона распределения. В противоположность функции распределения эта форма не является универсальной, она существует только для н.с.в.
 f(x)
f(x)
 |
 Х
Х
Рассмотрим непрерывную случайную величину с плотностью распределения и элементарный участок dx, примыкающий к точке x. Вероятность попадания случайной величины X на этот участок равна f(x)d(x ). Величина f(x)dx называется элементом вероятности. Геометрически это есть площадь элементарного прямоугольника, опирающегося на отрезок dx (Рис. 1).
 f (x) f (x)
f (x) f (x)
 | |||||
 | |||||
 | |||||





 f(x)
f(x)

 X X
X X







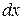
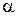
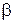
Рис.1 Рис.2
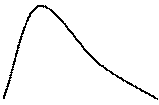
Выразим вероятность попадания величины Х на отрезок от  до
до 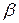 (Рис. 2) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
(Рис. 2) через плотность распределения. Очевидно, она равна сумме элементов вероятности на всем этом участке, т.е. интегралу:
Р( < X <
< X <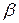 ) =
) = 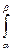 f(x)dx
f(x)dx
Геометрически вероятность попадания величины X на участок ( ,
, 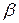 ) равна площади кривой распределения, опирающейся на этот участок. Если выразить функцию распределения через плотность, то:
) равна площади кривой распределения, опирающейся на этот участок. Если выразить функцию распределения через плотность, то:
F (x) = P (-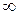 < X < x) =
< X < x) = 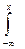 f(x)dx.
f(x)dx.
Геометрически F(x) есть площадь кривой распределения, лежащая левее точки x.

 f(x)
f(x)






 х Х
х Х
Укажем основные свойства плотности распределения:
1. Плотность распределения есть неотрицательная функция: f(x)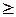 0. Это свойство вытекает непосредственно из того, что функция распределения есть неубывающая функция.
0. Это свойство вытекает непосредственно из того, что функция распределения есть неубывающая функция.
2. Интеграл в бесконечных пределах от плотности распределения равен единице: 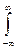 f(x)dx =1, так как F(
f(x)dx =1, так как F(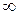 ) = 1.
) = 1.
Геометрически это означает, что площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Пример. Случайная величина Х распределена по закону "прямоугольного треугольника" в интервале (0,а). Необходимо: 
а) написать выражение плотности распределения;
б) найти функцию распределения F(x);
в) найти вероятность попадания случайной величины X на участке от a/2 до a.
Решение. Используем свойства линейной функции у = кх + в: к = -2/аа (площадь треугольника S = а/2, у = 2/а); к= -2/а2;
f(x) = 2/a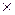 (1-x/a)
(1-x/a)
 f(x)
f(x)
 |


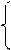 0 при x < 0;
0 при x < 0;

 f(x) = 2/a
f(x) = 2/a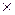 (1-x/a) при 0
(1-x/a) при 0 x
x a;
a;
 0 при x > 0.
0 при x > 0.
 X
X
 a
a

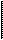 F(x) =
F(x) = 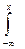 2/a
2/a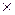 (1-x/a)dx = 2/a
(1-x/a)dx = 2/a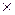 x- x2/a2 = x/a
x- x2/a2 = x/a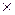 (2-x/a)
(2-x/a)  ;
;
 0 при х < 0;
0 при х < 0;
F(x) = x/a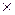 (2-x/a) при 0 < x < a;
(2-x/a) при 0 < x < a;
1 при х > a;
F(a) – F(a/2) =1 – 3/4 = 1/4.
 2014-02-24
2014-02-24 2521
2521
