Если две случайные величины х1 и х2 каждая в отдельности имеют нормальное распределение с параметрами М(х1), М(х2) и 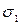 =
= 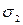 =
=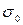 ,то модуль разности этих величин r =
,то модуль разности этих величин r =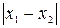 имеет распределение, которое носит название закона распределения модуля разности. Этому закону часто подчиняются погрешности взаимно расположенных поверхностей и осей, а также погрешности формы деталей: овальность, конусность и т.д.
имеет распределение, которое носит название закона распределения модуля разности. Этому закону часто подчиняются погрешности взаимно расположенных поверхностей и осей, а также погрешности формы деталей: овальность, конусность и т.д.
Плотность вероятности или дифференциальная функция распределения случайной величины r выражается следующим уравнением:
f(r) = 1/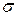 0
0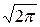 [ e- (r – M(x
[ e- (r – M(x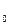 ))/
))/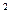 2
2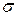
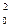 + e- (r +M(x
+ e- (r +M(x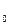 ))/
))/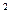 2
2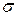
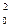 ],
],

 где М(х0) = М(х1) – М(х2) и
где М(х0) = М(х1) – М(х2) и 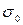 являются параметрами распределения модуля разности r.
являются параметрами распределения модуля разности r.
Интегральная функция распределения модуля разности имеет вид: F(r)) = 1/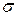 0
0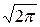
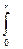 [ e- (r – M(x
[ e- (r – M(x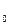 ))/
))/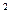 2
2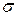
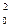 +
+
+ e- (r +M(x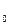 ))/
))/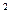 2
2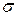
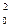 ],
],
Вид кривой распределения f(r) зависит от отношения M(x0)/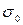 :
:

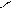
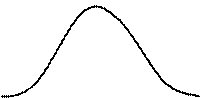
 f(r) M(x0)/
f(r) M(x0)/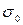 = 0
= 0

 M(x0)/
M(x0)/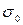 = 3
= 3
 |
 r
r
3.8. Композиция законов распределения.
Если величина U является суммой других взаимно независимых случайных величин X, Y, Z,...,то закон распределения суммы U называется композицией законов распределения слагаемых X, Y, Z,.... Операция нахождения закона называется компонированием и обозначается значком 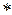 .
.
В случаях, когда суммируемые слагаемые X, Y, Z,... заданы вероятностями p1(xi), p2(yi), p3(zi),... или функциями F(x), F(y), F(z),... или плотностями вероятности f(x), f(y), f(z),... формулы компонирования записываются следующим образом:
P(Uk) = p1(xi)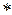 p2(yi)
p2(yi)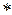 p3(zi)...;
p3(zi)...;
F(U) = F(x)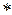 F(y)
F(y)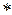 F(z)...;
F(z)...;
f(U) = f(x) f(y)
f(y)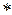 f(z)....
f(z)....
Закон распределения суммы нескольких слагаемых находится путем последовательного определения закона для суммы 2-х слагаемых, потом к этой сумме добавляется третье слагаемое и т.д.
Рассмотрим следующий пример. Дискретные случайные величины X и Y заданы рядами распределения
| Хi | 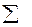 pi pi
| |||||
| P(Xi) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 | |
| Yi | ||||||
| P(Yi) | 1/5 | 1/5 | 1/5 | 1/5 | 1/5 |
Закон распределения суммы U двух независимых д.с.в. X и Y, заданных их законами распределения P(Xi) и P(Yi), определяется по следующей формуле композиции дискретных законов распределения:
P(Uk) = p(xi)p(yi) = 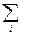 p1(xi)p2(uk – xi) =
p1(xi)p2(uk – xi) = 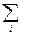 p1(yi)p2(uk – yi).
p1(yi)p2(uk – yi).
Определим область возможных значений величины U:
Umin = Xmin + Ymin = 2; Umax = Xmax + Ymax = 10;
Применяя способ непосредственного подсчета вероятностей и пользуясь основными теоремами о вероятностях, определим p(xi)p(yi). Расчеты удобно вести с помощью таблицы
| Uk | xi | yi | P(xi) | P(yi) | P(xi)P(yi) | P(u k) |
| 1/5 | 1/5 | 1/25 | 1/25 | |||
| 1/5 1/5 | 1/5 1/5 | 1/25 1/25 | 2/25 | |||
| 1/5 1/5 1/5 | 1/5 1/5 1/5 | 1/25 1/25 1/25 | 3/25 | |||
| 1/5 1/5 1/5 1/5 | 1/5 1/5 1/5 1/5 | 1/25 1/25 1/25 1/25 | 4/25 | |||
| 1/5 1/5 1/5 1/5 1/5 | 1/5 1/5 1/5 1/5 1/5 | 1/25 1/25 1/25 1/25 1/25 | 5/25 | |||
| 1/5 1/5 1/5 1/5 | 1/5 1/5 1/5 1/5 | 1/25 1/25 1/25 1/25 | 4/25 | |||
| 1/5 1/5 1/5 | 1/5 1/5 1/5 | 1/25 1/25 1/25 | 3/25 | |||
| 1/5 1/5 | 1/5 1/5 | 1/25 1/25 | 2/25 | |||
| 1/5 | 1/5 | 1/25 | 1/25 |
Составим ряд распределения случайной величины U:
| ui | |||||||||
| P(ui) | 1/25 | 2/25 | 3/25 | 4/25 | 5/25 | 4/25 | 3/25 | 2/25 | 1/25 |
Графическое представление результатов:
 P(x) P(y)
P(x) P(y)












 1/25 1/25
1/25 1/25

 1 2 3 4 5 X 1 2 3 4 5 Y
1 2 3 4 5 X 1 2 3 4 5 Y
 P(U)
P(U)

 5/25
5/25

 4/25
4/25


 3/25
3/25

 2/25
2/25
 1/25
1/25
 |  | ||
 1 2 3 4 5 6 7 8 9 10 U
1 2 3 4 5 6 7 8 9 10 U
Пример. Случайная величина Х распределена по нормальному закону с плотностью f(x) = (1/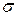
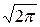 )e-[x-M(x)]
)e-[x-M(x)]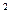 /2
/2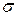
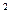 , случайная величина Y распределена по закону равной вероятности в интервале от а до в с плотностью f(y) = 1/(b – a).
, случайная величина Y распределена по закону равной вероятности в интервале от а до в с плотностью f(y) = 1/(b – a).
Плотность вероятности суммы U двух независимых случайных величин X и Y, заданных их плотностями вероятностей f1(x) и f2(y), определится по формуле:
f(u) = f(x+y) = f1(x)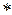 f(y) =
f(y) = 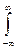 f1(x)f2(y) =
f1(x)f2(y) = 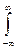 f1(x)f2(u – x)dx = =
f1(x)f2(u – x)dx = =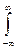 f2(y)f2(u – y)dy
f2(y)f2(u – y)dy
Для рассматриваемого примера уравнение примет конкретный вид:
f(u) = 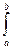 [1/(b – a)](1/
[1/(b – a)](1/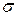
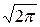 )e-[u – y – M(x)]
)e-[u – y – M(x)]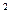 /2
/2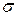
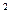 dy, a
dy, a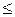 y
y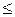 b.
b.
Здесь интеграл берется от a до b, потому что только в этих пределах y 0. Введем подстановку:
0. Введем подстановку:
[u – y – M (x)] /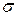 = – t; dy =
= – t; dy = 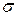 dt;
dt;
[a – u + M(x)] /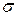 = t1; [b – u + M(x)] /
= t1; [b – u + M(x)] /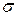 = t2;
= t2;
Тогда уравнение примет вид:
f(u) = (1/b – a)(1/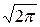 )
)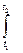 e-t
e-t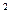 dt = 1/(b – a)[
dt = 1/(b – a)[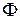 (t1) –
(t1) – 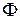 (t2) ],
(t2) ],
где 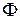 (t) – функция Лапласа.
(t) – функция Лапласа.
Так как среднее значение для х равно М(х), для y - (b + a)/2, то
M(u) = M(x) + (b + a)/2; D(u) = D(x) + (b – a)2/12.
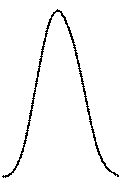
 f(u)
f(u) 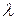 = 0
= 0


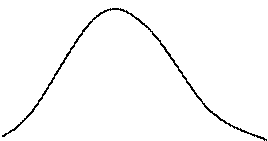 |



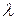 = 0,67
= 0,67
 |


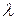 =2,2
=2,2
 u
u
На рисунке приведены кривые распределения по закону композиции нормального и равновероятного распределения при различных 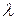 = (b – a)/
= (b – a)/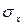 . Вид кривых показывает, что с уменьшением
. Вид кривых показывает, что с уменьшением 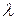 они приближаются к нормальной кривой. Поэтому, когда b – a
они приближаются к нормальной кривой. Поэтому, когда b – a 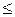
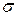 , для практических целей можно использовать закон нормального распределения.
, для практических целей можно использовать закон нормального распределения.
ЛЕКЦИЯ 4. ОСНОВЫ МАТЕМАТИЧЕСКОЙ
 2014-02-24
2014-02-24 2802
2802
