Наиболее надежный путь выявления закономерностей распределения — увеличение количества наблюдений. По мере увеличения количества наблюдений (в пределах той же однородной совокупности) при одновременном уменьшении величины интервала закономерность, характерная для данного распределения, будет выступать все более и более ясно, а представляющая полигон частот ломаная линия будет приближаться к некоторой плавной линии и в пределе должна превратиться в кривую линию.
Кривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения.
В настоящее время изучено значительное число различных форм распределений. В практике статистических исследований часто используется распределение Пуассона, Максвелла, особенно нормальное распределение. Распределения, близкие к нормальному распределению, были обнаружены при изучении самых различных явлений как в природе, так и в развитии общества.
Особенности кривой нормального распределения:
• кривая симметрична относительно максимальной ординаты, которая соответствует значению 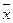 = Mo = Me, ее величина равна
= Mo = Me, ее величина равна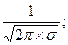
• кривая имеет две точки перегиба, находящиеся на расстоянии ±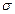 от
от 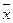 ;
;
• кривая асимптотически приближается к оси абсцисс, продолжаясь в обе стороны до бесконечности; чем больше значения отклонений от х, тем реже они встречаются;
• при 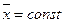 с увеличением
с увеличением 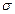 кривая становится более пологой; при
кривая становится более пологой; при 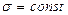 с изменением
с изменением 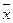 кривая не меняет свою форму, а лишь сдвигается влево или вправо по оси абсцисс;
кривая не меняет свою форму, а лишь сдвигается влево или вправо по оси абсцисс;
• в промежутке 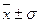 находится 68,3% всех значений признака; в промежутке
находится 68,3% всех значений признака; в промежутке 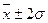 — 95,4% всех значений признака; в пределах
— 95,4% всех значений признака; в пределах 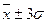 - 99,7% всех значений признака.
- 99,7% всех значений признака.
В статистической практике большой интерес представляет решение вопроса о том, в какой мере можно считать полученное в результате статистического наблюдения распределение признака в исследуемой совокупности, соответствующим нормальному распределению.
Для решения этого вопроса следует рассчитать теоретические
частоты нормального распределения, т. е. те частоты, которые
были бы, если бы данное распределение в точности следовало закону нормального распределения. Для расчета теоретических частот применяется формула:
 (5.46)
(5.46)
где 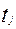 — нормированное отклонение;
— нормированное отклонение;
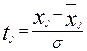 . (5.47)
. (5.47)
Величина 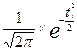 определяется по специальной таблице (см. приложение 1 Практикума).
определяется по специальной таблице (см. приложение 1 Практикума).
Следовательно, в зависимости от величины 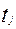 для каждого интервала эмпирического ряда определяются теоретические частоты (графа 9 табл. 5.2).
для каждого интервала эмпирического ряда определяются теоретические частоты (графа 9 табл. 5.2).
Для проверки близости теоретического и эмпирического распределений используются специальные показатели, называемые критериями согласия. Наиболее распространенным является критерий согласия К. Пирсона 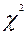 («хи-квадрат»), исчисляемый по формуле:
(«хи-квадрат»), исчисляемый по формуле:
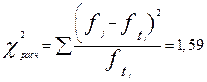 , (5.48)
, (5.48)
где 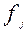 — эмпирические частоты (частости) в интервале;
— эмпирические частоты (частости) в интервале;
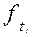 — теоретические частоты (частости) в интервале.
— теоретические частоты (частости) в интервале.
Полученное расчётное значение критерия сравнивается с табличным значением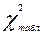 , которое определяется по специальной таблице (см. приложение 2 Практикума) в зависимости от принятой вероятности (Р) и числа степеней свободы к (для нормального распределения к равно числу групп в ряду распределения минус 3). Для рассматриваемого примера k=2; P =0,95;
, которое определяется по специальной таблице (см. приложение 2 Практикума) в зависимости от принятой вероятности (Р) и числа степеней свободы к (для нормального распределения к равно числу групп в ряду распределения минус 3). Для рассматриваемого примера k=2; P =0,95;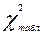 =5,99.
=5,99.
Если 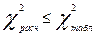 , то гипотеза о близости эмпирического распределения к нормальному не отвергается.
, то гипотеза о близости эмпирического распределения к нормальному не отвергается.
При расчете критерия Пирсона необходимо соблюдать условия: число наблюдений должно быть достаточно велико (n > 50); если теоретические частоты в некоторых интервалах меньше 5, то интервалы объединяют так, чтобы частоты были больше 5.
Используя величину 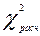 В. И. Романовский предложил оценивать близость эмпирического распределения кривой нормального распределения по критерию:
В. И. Романовский предложил оценивать близость эмпирического распределения кривой нормального распределения по критерию:
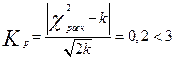 , (5.49) где
, (5.49) где  - число степеней свободы;
- число степеней свободы;
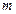 — число групп;
— число групп;
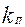 —количество параметров в теоретическом законе распределения (для нормального закона распределения
—количество параметров в теоретическом законе распределения (для нормального закона распределения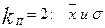 );
);
В данном примере расчётное значение критерия равно 0,2, следовательно можно принять гипотезу о нормальном характере эмпирического распределения.
Критерий А. Н. Колмогорова основан на определении максимального (по модулю) расхождения между накопленными частотами эмпирического и теоретического распределений (d),графа 11 табл. 5.2:
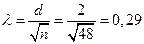 (5.50)
(5.50)
Необходимым условием использования критерия А.Н. Колмогорова является достаточно большое число наблюдений (не менее 100).
По таблице значений вероятностей 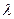 - критерия находят соответствующую вероятность (Р). Если найденной величине
- критерия находят соответствующую вероятность (Р). Если найденной величине 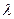 соответствует значительная по величине вероятность (Р), то расхождения между эмпирическим и теоретическим распределениями несущественны (см. табл. 1 Приложения к лекции, Р = 0,999).
соответствует значительная по величине вероятность (Р), то расхождения между эмпирическим и теоретическим распределениями несущественны (см. табл. 1 Приложения к лекции, Р = 0,999).
Кроме перечисленных критериев согласия оценить соответствие эмпирического распределения как сгрупированных так и не сгруппированных данных нормальному закону можно проверкой выполнения неравенств:
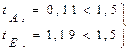 . (5.51)
. (5.51)
Отметим, что для рассматриваемой задачи оба неравенства выполняются.
Практическое и научное значение имеет распределение Пуассона. Оно характерно для редко встречающихся явлений, поэтому его называют «законом редких явлений» (или «законом малых чисел»).
Закон Пуассона применяется для совокупностей, достаточно больших по объему (n > 100) и имеющих достаточно малую долю единиц, обладающих данным признаком (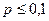 ), например для распределения партий готовой продукции по числу забракованных изделий, печатных страниц по числу опечаток, станков по числу отказов, ткацких станков по числу обрывов нити и т. д.
), например для распределения партий готовой продукции по числу забракованных изделий, печатных страниц по числу опечаток, станков по числу отказов, ткацких станков по числу обрывов нити и т. д.
Теоретические частоты распределения Пуассона определяются формулой:
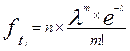 , (5.52)
, (5.52)
где 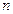 - общее число независимых испытаний;
- общее число независимых испытаний;
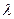 - среднее число появления редкого события в
- среднее число появления редкого события в 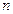 одинаковых независимых испытаниях;
одинаковых независимых испытаниях;
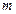 — частота данного события (
— частота данного события (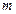 = 0,1,2,...);
= 0,1,2,...);
е — основание натуральных логарифмов, е = 2,71828.
Величина  определяется по специальной таблице (приложение 8);
определяется по специальной таблице (приложение 8);
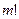 - произведение 1*2* 3... *
- произведение 1*2* 3... *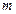 ; 0! - считается равным единице.
; 0! - считается равным единице.
Степень расхождения теоретических и эмпирических частот оценивается с помощью критериев согласия.
 2014-02-04
2014-02-04 1267
1267
