Статистический анализ с помощью точечных

диаграмм (статистическое регулирование качества)

Статистический анализ технологических процессов с помощью малых выборок требует довольно значительного количества вычислительных работ, связанных с проверкой гипотез однородности средних и дисперсий выборок. Поэтому в производственных условиях наиболее удобным и простым является метод точечных диаграмм. Техническим вспомогательным средством статистического регулирования является контрольная карта, позволяющая наглядно отразить ход производственного процесса. Различают контрольные карты по измеримым (количественным) и неизмеримым (качественным) признакам качества в зависимости от того, поддается ли количественному измерению признак или же допускает только качественную оценку.

К важнейшим видам контрольных карт по количественному признаку относятся следующие:

карта средних значений (карта «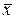»), карта индивидуальных значений, карта медиан и комбинированные контрольные карты, к которым относятся карта «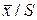», карта «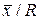», карта «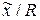» (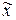- медиана ряда измерений). Что касается контрольных карт по неизмеримым качественным признакам, то здесь различают в основном 2 типа: карта «Р» -% или доля брака в партии, карта «С» - число дефектов в единице продукции.

9.4.1. Карта средних значений (карта «»)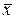

На примере карты средних значений, нашедшей широкое распространение будут изложены общие принципы техники контрольных карт, т.е. их построения и способа их ведения.

Пример. Изготавливается деталь с размером .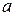

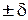Построить карту «».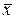

Для этой цели на графике вычерчивают среднюю линию а и определяют границы регулирования

; .

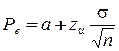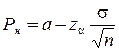где - верхняя, нижняя граница регулирования;

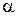- уровень значимости;

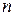- объем выборки.

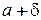
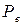
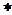
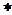
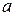
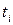
1 2 3 4 5 6 7

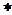
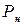
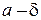
На графике вычерчивают среднюю линию а и границы регулирования 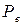и 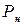. По оси абсцисс на равных расстояниях откладывают мо­менты времени 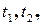... отбора n деталей, а по оси ординат в соответствующем масштабе наносятся средние арифметические значения 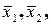... рассчитанные по измерениям. Это и есть карта средних значений. Регулирование процесса производится следующим образом: в установленные моменты времени 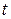(i = 1,2...) отбирается n изделий, изготовленных на станке, прессе и рассчитывают по ним среднее арифметическое 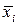, которое для соответствующего 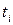наносится на контрольную карту в виде точки или крестика. До тех пор, пока такая точка находится внутри контрольных границ, оборудование обеспечивает требуемый размер. Если, кроме того, не нарушены границы допуска, процесс находится в статистически подконтрольном состоянии.

Появление значения ординаты 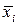, расположенной над верхней границей 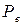или под нижней границей 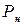расценивается как сигнал к остановке производственного процесса и проверке настройки станка. Процесс находится в неподконтрольном состоянии.

При построении всякой контрольной карты важнейшей задачей является расчет границ регулирования 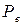и 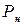. Эти границы зависят от характеристик производственного процесса - от номинального размера а и дисперсии . Дисперсия определяется опытным путем методом больших выборок.

Значения 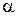и n заранее фиксируются. Величину 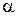в случае распределения размеров по нормальному закону принимают равной 0,0027. В этом случае 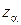= 3 и формулы для расчета границ регулирования примут вид

.

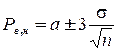В общем случае значение 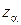можно выбрать по таблице

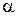
	0,001	0,0027	0.01	0,0455	0,05
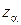
	3,291	3,0	2,576	2,0	1,96

Рекомендуется выдерживать постоянный объем выборки n, так как в противном случае необходимо всякий раз пересчитывать границы регулирования. На практике обычно используют величины n = 4;5;6;7.

9.4.2. Карта медиан (карта )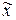

При ведении карты медиан вместо среднего арифметического используется медиана или срединное значение 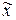ряда измерений, что позволяет существенно упростить расчеты. Для таких карт необходимо выбирать нечетный объем пробы (n=5; 7), так как в этом случае легко на карте найти и отметить медиану, как 3-е или 4-е значение.

Формулы для расчета границ регулирования

.

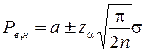По сравнению с картой средних значений карта медиан обладает тем преимуществом, что для ее ведения необходимо значительно меньше вычислений, а это очень важно для практики. Однако она менее эффективна, чем карта 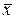, ее контрольные интервалы несколько шире, так как дисперсия медианы больше дисперсии среднего арифметического.

9.4.3. Карты «»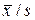

Для характеристики процесса одной величины далеко недостаточно. Кроме того, важно знать рассеивание или разброс отдельных значений и их изменение во времени в ходе производственного процесса. В связи с этим в технике контрольных карт принимают совместно с картой «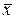» или «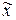» карту «S» - среднее квадратичное отклонение или «R» - размах.

Расчет границ регулирования для карты «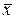» - прежний.

Границы регулирования для карты «S» (определяется только верхняя граница, так как нижнюю определять нет смысла):

.

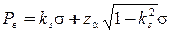Для 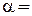0,0027 и 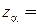3 формула примет вид

.

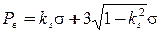Значение 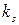для 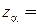3 по таблице

Таблица коэффициентов

n
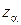
	0,798	0,886	0,921	0,940	0,952
n
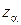
	0,959	0,965	0,969	0,973

После расчета контрольных границ обеих карт начинается систематическое наблюдение за производственным процессом. С оборудования (станок, пресс) периодически снимают последние n изделий, замеряют нужный признак, рассчитывают по n измерениям среднее арифметическое 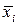и среднее квадратическое S (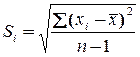) и наносят обе величины соответственно на карты «» и «S». Вмешательство в ход процесса регулирования его имеет место, когда одно из значений : выходит за верхнюю границу карты «S». Основной недостаток карт - большой объем вычислений.