Линии и трубки тока. Неразрывность струи

При изучении жидкостей их рассматривают как сплошную непрерывную среду, не вдаваясь в молекулярное строение жидкостей. При описании движения жидкости проще следить не за частицами жидкости, а за отдельными точками пространства и отмечать скорость, с которой проходят через каждую точку отдельные частицы.

Графически движение жидкостей изображается с помощью линий тока, которые проводятся так, что касательные к ним совпадают по направлению с вектором скорости жидкости в каждой точке пространства.

Условимся проводить линии тока так, чтобы густота их была пропорциональна

Рис.1

величине скорости в данном месте. Тогда по картине линий тока можно будет судить не только о направлении, но и о величине вектора скорости в разных точках пространства (рис.1). Например, в точке А густота линий, а следовательно и модуль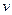, больше, чем в точке В.

Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Течение жидкости называется установившимся (или стационарным), если вектор скорости в каждой точке пространства остается постоянным. При стационарном течении любая частица жидкости проходит данную точку пространства с одной и той же скоростью 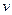. Картина линий тока при стационарном течении остается неизменной, и линии тока совпадают с траекториями частиц.

Рассмотрим трубку тока, выберем два ее сечения 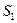и 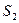, перпендикулярные направлению скорости. Предположим, что во всех точках сечения скорость частиц

Рис.2

жидкости одинакова. За одну секунду через сечение 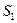пройдет объем жидкости 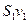, а через сечение 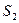- 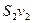(рис.2). Если жидкость несжимаема (то есть плотность ее всюду постоянна), то количество жидкости между сечениям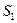и и 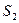будет оставаться неизменным. Отсюда следует, что объемы жидкости, протекающие за единицу времени через сечения 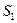и 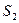должны быть одинаковы

= .

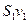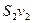Следовательно для несжимаемой жидкости при стационарном течении величина 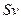в любом сечении данной трубки должна быть одинакова

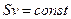
Это выражение есть теорема о неразрывности струи. Из него следует, что при переменном сечении трубки тока частицы несжимаемой жидкости движутся с ускорением (см. рис.3)

	Теорема о неразрывности струи применима к реальным жидкостям и даже к газам в том случае, когда их сжимаемостью можно пренебречь. Расчеты показывают, что при движении жидкостей и газов со скоростями, меньшими скорости звука, их можно считать несжимаемыми.
Рис. 3