Изучение движения реальных жидкостей и газов представляет собой сложную задачу. Поэтому для ее упрощения пренебрегают силами внутреннего трения. Воображаемая жидкость, в которой полностью отсутствует внутреннее трение называется идеальной.
Рассмотрим стационарное течение несжимаемой идеальной жидкости. Выделим объем жидкости, ограниченный стенками узкой трубки тока и перпендикулярными к линиям тока сечениями 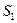 и
и 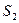 (рис.4). За время
(рис.4). За время 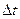 этот объем сместится вдоль трубки тока,
этот объем сместится вдоль трубки тока,
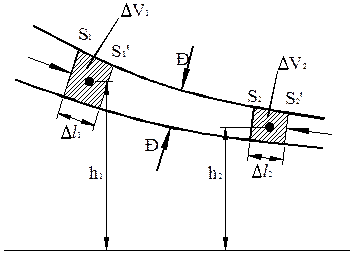 | причем граница 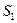 сместится к сместится к 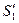 , получив перемещение , получив перемещение 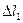 , а граница , а граница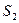 к к 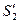 , получив перемещение , получив перемещение 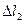 . Работа, совершаемая при этом силами давления, равна приращению полной энергии в рассматриваемом объеме жидкости. Силы давления на стенки трубки тока перпендикулярны в каждой точке к направлению перемещения жидкости, и . Работа, совершаемая при этом силами давления, равна приращению полной энергии в рассматриваемом объеме жидкости. Силы давления на стенки трубки тока перпендикулярны в каждой точке к направлению перемещения жидкости, и |
поэтому работы не совершают. Отлична от нуля только работа сил давления, приложенная к сечениям 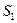 и
и 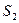 . Эта работа равна
. Эта работа равна
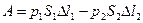 =
= 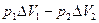 (1)
(1)
Вследствие несжимаемости жидкости за время 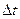 через сечения
через сечения 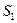 и
и 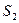 пройдет один и тот же объем жидкости, то есть
пройдет один и тот же объем жидкости, то есть 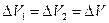 . Тогда выражение (1) примет вид
. Тогда выражение (1) примет вид
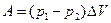 (2)
(2)
Полная энергия рассматриваемого объема жидкости складывается из кинетической энергии и потенциальной энергии в поле сил земного тяготения. Вследствие стационарности течения полная энергия жидкости между сечениями 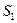 и
и 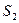 за время
за время 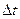 изменится за счет работы. Поэтому приращение полной энергии рассматриваемого объема равно разности значений полной энергии объемов
изменится за счет работы. Поэтому приращение полной энергии рассматриваемого объема равно разности значений полной энергии объемов 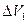 и
и 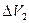 , масса которых
, масса которых 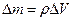 ,
, 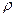 .- плотность жидкости.
.- плотность жидкости.
Возьмем сечение 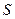 трубки тока и перемещение
трубки тока и перемещение 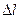 настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости
настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости 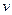 , давления
, давления 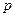 и высоты
и высоты 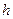 Тогда для приращения полной энергии получается выражение
Тогда для приращения полной энергии получается выражение
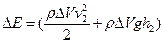 -
- 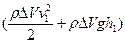 (3)
(3)
Приравнивая выражения (2) и (3), сокращая на 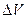 и перенося члены с одинаковыми индексами в одну часть равенства, получим
и перенося члены с одинаковыми индексами в одну часть равенства, получим
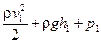 =
= 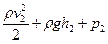 (4)
(4)
Сечения 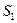 и
и 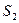 выбирались произвольно, поэтому для любого сечения
выбирались произвольно, поэтому для любого сечения
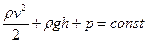 (5)
(5)
Выражение (5) выведено швейцарским физиком Даниилом Бернулли и получило название – уравнение Бернулли.
Несмотря на то, что уравнение выведено для идеальной жидкости, оно применимо для реальных жидкостей, внутреннее трение которых не очень велико.
Величина 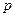 в формуле (5) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина
в формуле (5) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела), величина 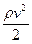 - динамическим давлением, а величина
- динамическим давлением, а величина 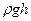 - гидростатическим давлением. Для горизонтальной трубки тока выражение (5) принимает вид
- гидростатическим давлением. Для горизонтальной трубки тока выражение (5) принимает вид
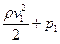 =
= 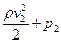 , (6)
, (6)
то есть давление оказывается меньшим в тех точках, где скорость больше.
Уменьшение давления в точках, где скорость больше, положено в основу устройства водоструйного насоса (см. рис. 5)
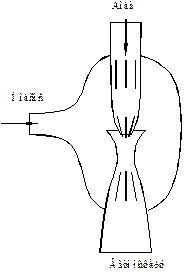 | Струя воды подается в трубку, открывающуюся в атмосферу, так что на выходе из трубки давление равно атмосферному. В трубке имеется сужение, по которому вода идет с большой скоростью, поэтому давление в этом месте оказывается меньше атмосферного. Такое давление устанавливается и в охватывающей трубку камере насоса, которая сообщается с трубкой через разрыв, имеющийся в узкой части трубка. Подсоединив к камере насоса откачиваемый объем, из него можно откачать воздух до давления порядка 100 мм рт. ст. (ртутного столба). |
| Рис. 5. |
Сумма статического 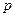 и динамического давления
и динамического давления 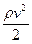 называется полным давлением
называется полным давлением
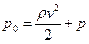 .
.
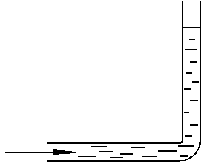 | Для измерения полного давления используется трубка Пито. Это небольшая изогнутая манометрическая трубка, обращенная открытым концом навстречу потоку жидкости (см. рис. 6) Линии тока, направленные к трубке Пито, заканчиваются внутри трубки, где жидкость покоится, то есть скорость жидкости изменяется от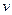 до 0. Высота столба жидкости, устанавливающаяся в трубке является поэтому мерой максимального давления, то есть полного напора жидкости до 0. Высота столба жидкости, устанавливающаяся в трубке является поэтому мерой максимального давления, то есть полного напора жидкости 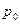 . . |
| Рис.6. |
Для измерения статического давления 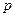 в поток вводят изогнутую трубку с закрытым концом и боковым отверстием (см. рис.7).
в поток вводят изогнутую трубку с закрытым концом и боковым отверстием (см. рис.7).
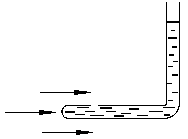 | Такая трубка называется зондом. Скорость жидкости вблизи отверстия (а следовательно и давление) будет мало отличаться от скорости (и давления) в невозмущенном потоке. Поэтому манометр, присоединенный к зонду покажет статическое давление 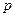 . . |
| Рис. 7 |
Прандтль трубку Пито соединил с зондом (см. рис. 8) Получившийся прибор измеряет
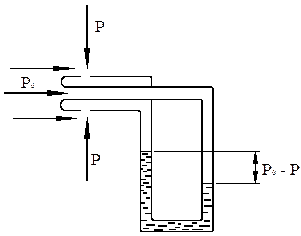 | разность полного и статистического давления, то есть динамическое давление 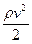 . Для заданной плотности манометр можно проградуировать в значениях скорости. Поэтому трубка Пито-Прандтля может служить прибором для измерения скорости течения жидкости или газа. . Для заданной плотности манометр можно проградуировать в значениях скорости. Поэтому трубка Пито-Прандтля может служить прибором для измерения скорости течения жидкости или газа. |
| Рис.8. |
 2014-02-09
2014-02-09 1302
1302








