Из определения числа Био следует, что его очень большие значения могут иметь место в основном при очень больших коэффициентах теплоотдачи, а также при больших размерах толщины пластины и малых значениях коэффициента теплопроводности. Поэтому нагрев при больших числах Био (практически при Bi≥100) принято называть нагревом "термически массивного" тела (ТМТ). Примеры таких тел: закалка изделий в жидких расплавах, разогрев массивных огнеупорных футеровок нагревательных и других печей, стале- и чугуноразливочных ковшей.
При больших числах Био температура поверхности пластины почти сразу становится равной температуре окружающей среды, в которую она помещена.
При больших числах Био для определения первого корня следует вместо (3.9) пользоваться уравнением (3.12):
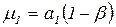 , (3.64)
, (3.64)
где 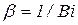 - перевернутое число Био;
- перевернутое число Био; 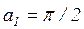 .
.
Начальная тепловая амплитуда с учетом (3.64) станет
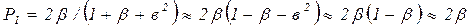 , (3.65)
, (3.65)
где 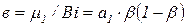 .
.
Амплитуда для расчета среднемассовой температуры при больших Био
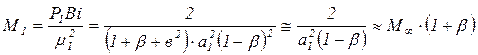 , (3.66)
, (3.66)
где 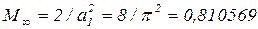 - минимальное значение амплитуды М1, которое получается в предельном случае
- минимальное значение амплитуды М1, которое получается в предельном случае 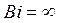 .
.
Для расчета центральной амплитуды предварительно получим уравнение, аналогичное (3.42), но пригодное для расчетов при больших Био.
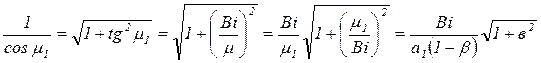 (3.67)
(3.67)
Тогда
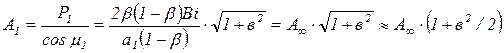 , (3.68)
, (3.68)
где 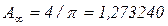 - максимальное предельное значение А1 при
- максимальное предельное значение А1 при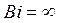 .
.
Далее расчет нагрева (охлаждения) ТМТ производится по уравнениям (3.19)…(3.22) в стадии РРН, но с учетом асимптотических выражений (3.64)…(3.68), удобных для вычислений при больших числах Био.
Так, например, расчеты по формулам (3.21) и (3.60) при 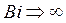 приводит к неопределенности типа 0/0 и
приводит к неопределенности типа 0/0 и 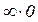 , однако использование выражений (3.66)…(3.68) устраняет указанные недостатки.
, однако использование выражений (3.66)…(3.68) устраняет указанные недостатки.
Уравнение (3.15) по расчету температур в центре с учетом (3.68) преобразуется к виду
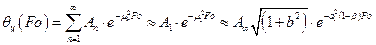 , (3.69)
, (3.69)
а уравнение для среднемассовой с учетом (3.66) станет
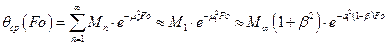 , (3.70)
, (3.70)
где 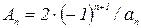 ;
; 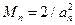 ;
; 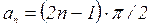 ;
;
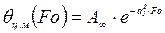 ,
, 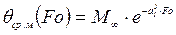 - центральная и среднемассовая температуры соответственно для “чисто массивного” тела, нагреваемого в режиме
- центральная и среднемассовая температуры соответственно для “чисто массивного” тела, нагреваемого в режиме 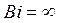
 или
или 
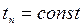 .
.
Формулы для расчета времени нагрева при больших числах Био преобразуются следующим образом.
Уравнение (3.34) с учетом (3.64) и (3.66) примет вид
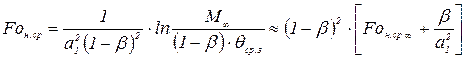 , (3.71)
, (3.71)
а уравнение (3.35) с учетом (3.68) станет
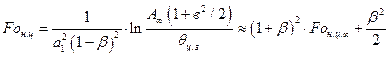 . (3.72)
. (3.72)
Следует отметить весьма характерную особенность, возникающую при расчетах времени нагрева по формулам (3.71) и (3.72). Если при расчете времени нагрева до заданной температуры (3.32) поверхности вести по выражению (3.36), то получается естественный результат и вывод: с ростом числа Био время нагрева уменьшается и стремится к нулю при 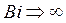 . Однако, при расчетах времени нагрева до заданных среднемассовой и центральной температур существует минимально возможные времена нагрева, которые получаются из уравнений (3.71), (3.72) в предельном случае при
. Однако, при расчетах времени нагрева до заданных среднемассовой и центральной температур существует минимально возможные времена нагрева, которые получаются из уравнений (3.71), (3.72) в предельном случае при 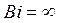
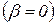
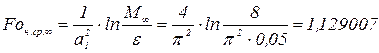 (3.73)
(3.73)
и
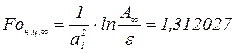 (3.74)
(3.74)
ниже которых время нагрева опуститься не может.
Получим формулы для расчета времени инерционного периода при больших числах Био. Обозначим через 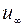 максимально возможное значение постоянной
максимально возможное значение постоянной 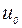 , которое определяется из уравнения (3.30) при
, которое определяется из уравнения (3.30) при 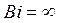 :
:
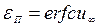 . (3.75)
. (3.75)
Например, при 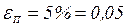 расчет на ЭВМ по уравнению (3.75) даст
расчет на ЭВМ по уравнению (3.75) даст 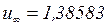 . По первому способу используем уравнение (3.30) и применим согласно [20] разложение функции ошибок в ряд
. По первому способу используем уравнение (3.30) и применим согласно [20] разложение функции ошибок в ряд 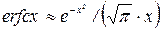 при больших аргументах, т. к. согласно (3.54) постоянная
при больших аргументах, т. к. согласно (3.54) постоянная 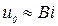 и следует ожидать, что
и следует ожидать, что 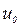 будет
будет 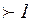 .
.
Уравнение (3.30) с учетом сказанного примет вид
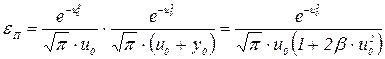 . (3.76)
. (3.76)
В пределе при 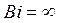 решение по уравнению (3.76) должно давать
решение по уравнению (3.76) должно давать 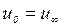 , поэтому можно предложить следующую приближенную формулу для расчета
, поэтому можно предложить следующую приближенную формулу для расчета 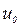 :
:
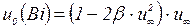 . (3.77)
. (3.77)
При известной 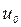 время инерционного периода легко определяется по уравнению (3.29)
время инерционного периода легко определяется по уравнению (3.29)
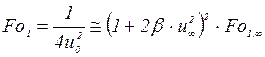 , (3.78)
, (3.78)
где 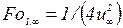 - время иррегулярного режима нагрева в случае
- время иррегулярного режима нагрева в случае 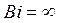 , при
, при 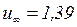
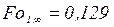 .
.
Найдем время 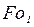 вторым способом из уравнения (3.72) для стадии РРН при
вторым способом из уравнения (3.72) для стадии РРН при 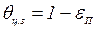 :
:
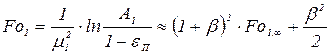 , (3.79)
, (3.79)
где 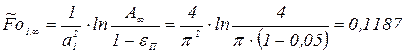 - минимальное предельное время, найденное из формул, описывающих регулярную стадию нагрева. Оценим степень различия величин, найденных различными способами, например, при степени прогрева
- минимальное предельное время, найденное из формул, описывающих регулярную стадию нагрева. Оценим степень различия величин, найденных различными способами, например, при степени прогрева 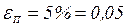 . Погрешность в определении постоянной
. Погрешность в определении постоянной 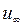 :
:
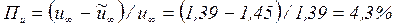 , а отличие при расчете инерционного времени
, а отличие при расчете инерционного времени 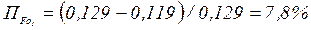 . Эти отличия можно объяснить тем, что при числах Фурье
. Эти отличия можно объяснить тем, что при числах Фурье 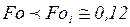 стадия РРН еще не наступила (это будет при
стадия РРН еще не наступила (это будет при 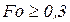 - см. уравнение (3.16)) и при расчетах следует брать два члена ряда (3.14).
- см. уравнение (3.16)) и при расчетах следует брать два члена ряда (3.14).
Усредним постоянную 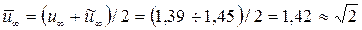 . Тогда, при расчетах
. Тогда, при расчетах 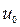 и
и 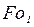 по формулам (3.77)…(3.79) можно принять
по формулам (3.77)…(3.79) можно принять 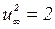 и
и 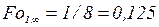 .
.
Результаты численного решения методом Ньютона [1] уравнения (3.75) при различных степенях прогрева 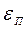 представлены в таблице 3.1. Там же приведены значения
представлены в таблице 3.1. Там же приведены значения 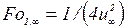 и для сравнения такие же величины, рассчитанные по уравнениям РРН (3.79) и
и для сравнения такие же величины, рассчитанные по уравнениям РРН (3.79) и 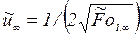 .
.
Таблица 3. 1 – Значения постоянной 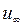 и времени инерционного
и времени инерционного
периода в зависимости от степени прогрева центральных точек тела при 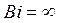 (
(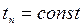 ).
).
Степень прогрева 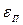 , % , %
| 0,5 | 1,0 | 5,0 | 10,0 | 15,0 | 20,0 |
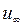
| 1,99 | 1,82 | 1,386 | 1,16 | 1,02 | 0,91 |
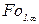
| 0,063 | 0,075 | 0,129 | 0,186 | 0,240 | 0,302 |
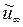
| 1,58 | 1,57 | 1,451 | 1,33 | 1,24 | 1,15 |
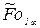
| 0,100 | 0,102 | 0,119 | 0,141 | 0,164 | 0,188 |
Оценим граничное число 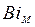 , когда тело можно считать термически массивным. Первая оценка
, когда тело можно считать термически массивным. Первая оценка 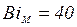 была найдена ранее из требования ограничения расчетов по формуле (3.33). С другой стороны, можно поступить аналогично как при установлении
была найдена ранее из требования ограничения расчетов по формуле (3.33). С другой стороны, можно поступить аналогично как при установлении 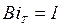 когда тело считается термически тонким. Положим Bi=10 и найдем погрешности расчетов по формулам (3.64)…(3.68) по сравнению с точным решением. Тогда, при
когда тело считается термически тонким. Положим Bi=10 и найдем погрешности расчетов по формулам (3.64)…(3.68) по сравнению с точным решением. Тогда, при 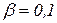 первый корень
первый корень 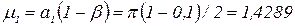 и погрешность
и погрешность 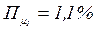 . Далее
. Далее 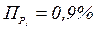 ,
, 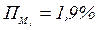 и
и 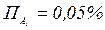 .
.
Таким образом, максимальная погрешность (как и ранее при малых числах Био) наблюдается при расчетах М1 и не превышает 2% и следовательно, термически массивным можно считать нагрев при 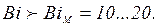
При средних числах Био, когда 0,1≤Вi≤100 для расчетов следует использовать более сложные общие решения (3.4, 3.7, 3.13…3.19).
После расчета безразмерных величин делается переход к размерным, согласно формулам их определения:
- для температур t = tж +(t0 – tж) × q, °C;
- для времени t = Fо× d 2/ a, с. (3.80)
 2014-02-24
2014-02-24 2051
2051








