При малых временах процесса 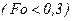 имеем иррегулярный или инерционный период нагрева, когда температура в центральных точках тела вследствие тепловой инерции практически равна начальной температуре
имеем иррегулярный или инерционный период нагрева, когда температура в центральных точках тела вследствие тепловой инерции практически равна начальной температуре 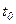 , т. е.
, т. е. 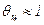 .
.
При очень малых числах Фурье 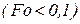 расчёт температур по уравнению (3.4) затруднителен из-за необходимости учёта большого количества членов ряда, ввиду его плохой сходимости. В этом случае можно использовать решение, полученное методом операционного исчисления для малых времен процесса в работе [3]:
расчёт температур по уравнению (3.4) затруднителен из-за необходимости учёта большого количества членов ряда, ввиду его плохой сходимости. В этом случае можно использовать решение, полученное методом операционного исчисления для малых времен процесса в работе [3]:
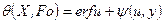 , (3.24)
, (3.24)
где 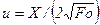 ;
; 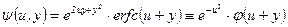 .
.
Полагая в уравнении (3.24) 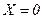
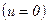 , получим выражение для расчета поверхностной температуры на начальной стадии нагрева
, получим выражение для расчета поверхностной температуры на начальной стадии нагрева
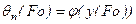 , (3.25)
, (3.25)
где 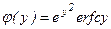 ;
;
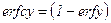 – дополнительный интеграл вероятностей;
– дополнительный интеграл вероятностей;
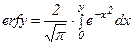 - функция ошибок Гаусса;
- функция ошибок Гаусса;
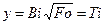 - безразмерное время, число Тихонова, может быть записано также в виде:
- безразмерное время, число Тихонова, может быть записано также в виде: 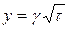 , где
, где 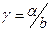 - служит мерой тепловой инерции, с-0,5;
- служит мерой тепловой инерции, с-0,5;
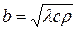 - коэффициент тепловой аккумуляции тела или коэффициент теплоусвоения, Вт×с0,5/м2×К.
- коэффициент тепловой аккумуляции тела или коэффициент теплоусвоения, Вт×с0,5/м2×К.
Среднемассовую температуру на начальной стадии можно найти следующим образом. Разрешая уравнение теплового баланса (3.6) относительно средней температуры и используя формулу для определения количества теплоты через удельный тепловой поток
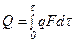 ,
,
где q определяется уравнением (2.4), получим
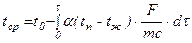
или в безразмерном виде
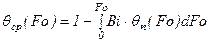 . (3.26)
. (3.26)
Подставляя в полученные соотношения температуру поверхности из уравнения (3.25) и интегрируя при постоянном числе Био, будем иметь
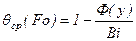 , (3.27)
, (3.27)
где 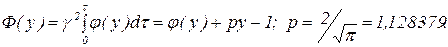
Следует отметить, что если в формуле (3.26) вместо (3.25) использовать уравнение (3.14), то можно получить точное решение (3.7).
Сопоставление приближенных зависимостей (3.25) и (3.27) с точными решениями (3.14) и (3.7) показало, что погрешность уравнения (3.27) при расчете средней температуры гораздо меньше, чем уравнения (3.25) для температуры поверхности.
Так, например, в случае нагрева при Bi=1 формулой (3.25) можно пользоваться с относительной погрешностью 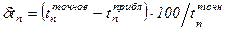 менее + 5% при времени начальной стадии Foн.с=0,5, а формулой (3.27) с погрешностью
менее + 5% при времени начальной стадии Foн.с=0,5, а формулой (3.27) с погрешностью 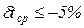 до момента времени Foн.с=1,0. Здесь под
до момента времени Foн.с=1,0. Здесь под 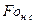 понимается время, до которого можно пользоваться формулами начальной стадии.
понимается время, до которого можно пользоваться формулами начальной стадии.
Решения (3.25) и (3.27) можно упростить путём разложения функции 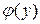 в ряд при малых (
в ряд при малых (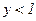 ):
): 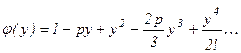
и при больших (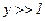 ) аргументах:
) аргументах: 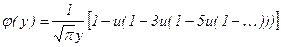 ,
,
где 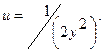
Графическое решение уравнений (3.25) и (3.27) приведено на рисунке 3.4.
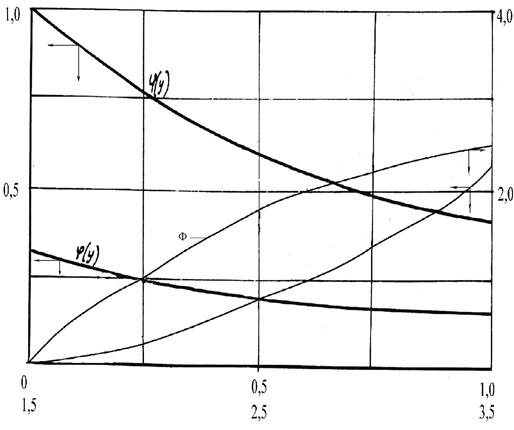
Рисунок 3.4 – Зависимость функций j и Ф от времени 
Интересно отметить, что, в отличие от уравнения (3.14), где температура поверхности зависит от двух величин – числа Био и Фурье, из уравнения (3.25) следует, что qп зависит только от одного параметра – числа Тихонова и вместо семейства кривых на рисунке 3.3, на рисунке 3.4 имеем всего одну линию. Решения, подобные (3.25), когда исчезает зависимость процесса от какого-либо параметра, принято называть автомодельными.
Для оценки времени инерционного периода нагрева 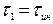 поступим следующим образом. При протекании высокоинтенсивных процессов нагрева (охлаждения) в теории теплопроводности вводится понятие глубины теплового возмущения или толщины прогретого слоя dп(t), т.е. расстояние от поверхности тела до точек, где температура еще остается равной первоначальной t0 или отличается от нее не более, чем, например, на e = 5%. Точных формул для расчета текущей толщины прогретой зоны нет, а из приближенных можно рекомендовать формулы, полученные профессором Постольником Ю. С. [14]:
поступим следующим образом. При протекании высокоинтенсивных процессов нагрева (охлаждения) в теории теплопроводности вводится понятие глубины теплового возмущения или толщины прогретого слоя dп(t), т.е. расстояние от поверхности тела до точек, где температура еще остается равной первоначальной t0 или отличается от нее не более, чем, например, на e = 5%. Точных формул для расчета текущей толщины прогретой зоны нет, а из приближенных можно рекомендовать формулы, полученные профессором Постольником Ю. С. [14]:
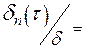 æ
æ 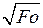
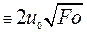 , (3.28)
, (3.28)
где æ 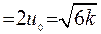 –для малых чисел Био (Ві<<2)
–для малых чисел Био (Ві<<2)
и æ 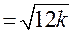 – для больших Био (Ві>>2);
– для больших Био (Ві>>2);
 k – фактор геометрической формы, равный 1, 2, 3 для плоских, цилиндрических и шаровых тел соответственно.
k – фактор геометрической формы, равный 1, 2, 3 для плоских, цилиндрических и шаровых тел соответственно.
Естественно полагать, что инерционный период нагрева закончится тогда, когда глубина теплового возмущения достигнет центральных точек тела. Полагая в уравнении (3.28) dп(t) = d, получим
Fо1 = 1 / æ2 =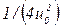 . (3.29)
. (3.29)
Для более точного расчета времени инерционного периода 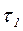 поступим следующим образом. Примем, что динамика изменения толщины прогретого слоя определяется выражением (3.28), в котором æ
поступим следующим образом. Примем, что динамика изменения толщины прогретого слоя определяется выражением (3.28), в котором æ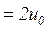 , а
, а 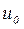 -безразмерная постоянная, зависящая от граничных условий на поверхности. Этот закон “квадратного корня” естественным образом вытекает из анализа температурного поля, в нашем случае из выражения (3.24) для полубесконечного плоского тела. Постоянная
-безразмерная постоянная, зависящая от граничных условий на поверхности. Этот закон “квадратного корня” естественным образом вытекает из анализа температурного поля, в нашем случае из выражения (3.24) для полубесконечного плоского тела. Постоянная 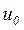 находится из уравнения (3.24) после замены в нем текущей пространственной координаты
находится из уравнения (3.24) после замены в нем текущей пространственной координаты 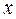 на глубину прогретого слоя
на глубину прогретого слоя 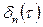 , числа Тихонова
, числа Тихонова 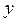 на
на 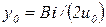 и относительной температуры в этой точке на малую величину степени прогрева
и относительной температуры в этой точке на малую величину степени прогрева 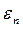 :
:
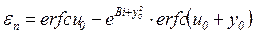 . (3.30)
. (3.30)
После определения постоянной 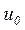 из трансцендентного уравнения (3.30) инерционное время нагрева легко находится из соотношения (3.29).
из трансцендентного уравнения (3.30) инерционное время нагрева легко находится из соотношения (3.29).
Если время 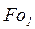 было найдено из каких-либо других условий, то постоянная
было найдено из каких-либо других условий, то постоянная
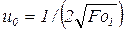 . (3.31)
. (3.31)
При практических расчетах возникает необходимость решать как прямую, когда по числу Био и Фурье отыскиваются температуры, так и обратную задачу, когда определяется время нагрева пластины до заданной температуры, например, на поверхности tп.з. Из уравнений (3.4), (3.7), (3.14)…(3.22) следует, что конец процесса нагрева (охлаждения), когда температура тела станет равна температуре окружающей среды (жидкости) 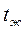 , достигается за бесконечно большой промежуток времени
, достигается за бесконечно большой промежуток времени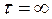 . Однако, практически процесс можно считать законченным, когда температура будет на малую заданную величину
. Однако, практически процесс можно считать законченным, когда температура будет на малую заданную величину 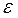 (например,
(например, 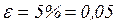 ) отличаться от температуры
) отличаться от температуры 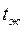 , т. е., например, температура поверхности достигает заданных технологией значений
, т. е., например, температура поверхности достигает заданных технологией значений 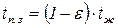 или в безразмерном виде:
или в безразмерном виде:
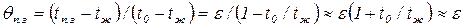 . (3.32)
. (3.32)
Прямая задача легко решается с помощью уравнений (3.4, 3.14…3.27) или рисунков 3.2 и 3.3, а для обратной задачи следует разрешать уравнения (3.14…3.22) относительно числа Фурье. Например, в стадии регулярного режима нагрева (РРН), путем потенцирования уравнения (3.20) получим время нагрева до заданной температуры qп.з на поверхности
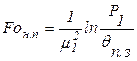 . (3.33)
. (3.33)
Аналогично можно получить времена нагрева, если заданы конечная среднемассовая qср.з:
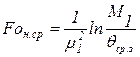 (3.34)
(3.34)
или в центре пластины qц.з
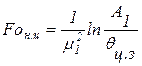 . (3.35)
. (3.35)
В случае, если окажется, что Fо < 0,3 (иррегулярный режим нагрева), можно получить формулу из уравнения (3.25) для предельных случаев больших и малых чисел Тихонова:
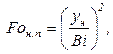 (3.36)
(3.36)
где 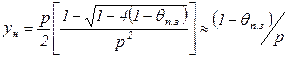 при малых y (y<1)
при малых y (y<1)
и 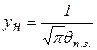 при больших y (y>>1).
при больших y (y>>1).
Покажем это на примере уравнения (3.33), расчет по которому может привести к отрицательному времени нагрева, если отношение 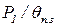 окажется меньше 1. Так как при больших числах Био
окажется меньше 1. Так как при больших числах Био 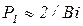 , следовательно формулой (3.33) можно пользоваться при числах
, следовательно формулой (3.33) можно пользоваться при числах 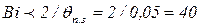 . При
. При 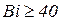 следует вести расчет не по (3.33),а по уравнению (3.36) в котором
следует вести расчет не по (3.33),а по уравнению (3.36) в котором 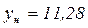 при
при 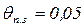 и будут получаться времена
и будут получаться времена 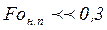 .
.
Для экспресс расчетов Fон.п можно обратиться к графикам на рисунках 3.2…3.4.
 2014-02-24
2014-02-24 1219
1219
