Основные понятия геометрии.
В
 А А
А А


Не имеет размера. Не имеет длинны. Не имеет границу.
| Планиметрия | Стереометрия | |||||||||||
| 1)Аксиомы расположения. | Выполняются все аксиомы планиметрии.
- Какова бы не была плоскость существуют точки лежащие в этой плоскости и не лежащие в ней.
   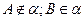
| |||||||||||
 а) А а А а) А а А а а
 В В 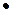 В В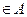
в) А В а - единственная |  б) А В С а
В лежит между А и С
г) б) А В С а
В лежит между А и С
г)
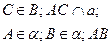
| |||||||||||
- Если две точки прямой принадлежат плоскости, то они пересекаются по прямо проходящей через эту точку.

Если А | ||||||||||||
| 2) Аксиомы измерения. | ||||||||||||
 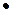 В AB=AC+CB
m С В AB=AC+CB
m С
 А А
 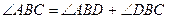
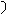  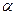 1800
1800
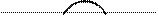 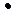  
| ||||||||||||
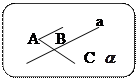
-Если две плоскости имеют общую точку, то они
пересекаются по прямо проходящей через эту точку.
| ||||||||||||
| 3) Аксиома откладывания | ||||||||||||
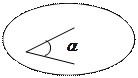
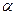 АВ = m АВ = m
    А В
АВ - единственный
А
А В
АВ - единственный
А 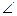 АВС= АВС=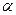
 А1 В1 А1 В1 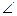 АВС – единств. АВС – единств.
 В С С1
В С С1
| ||||||||||||
-Через три любые точки не лежащие на одной прямой можно провести плоскость и только одну.
 А А
 В
С В
С
| ||||||||||||
Следовательно из третей аксиомы:
1.Через прямую и точку не лежащую на ней можно провести плоскость и только одну
- Через две пересекающиеся прямые можно провести плоскость и только одну.
| ||||||||||||
| 4) Аксиома параллельных прямых | ||||||||||||
- Через точку не лежащую на прямой можно провести одну и
только одну прямую параллельную данной.
 а
а II в а
а II в
 в
А в
А  А
А  в в - единственная в в - единственная
|
 2014-02-24
2014-02-24 1384
1384

 а
а




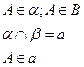
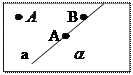


 -Через две параллельные прямые можно провести плоскость и только одну.
-Через две параллельные прямые можно провести плоскость и только одну.






