| Определение | Признак | Свойства | ||||||
| Прямая и плоскость | ||||||||
Прямая является параллельной плоскость, если не имеет общих точек с этой плоскостью.
  а
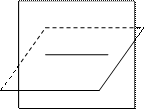
а II а
а II 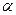
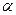
|    Если прямая не лежащая в плоскости параллельна прямой лежащей в плоскости, то она параллельна и самой плоскости
а аIIb; b Если прямая не лежащая в плоскости параллельна прямой лежащей в плоскости, то она параллельна и самой плоскости
а аIIb; b 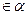 ;
а ;
а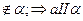 b
b
 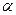
| Если плоскость проходит через прямую параллельную другой плоскости и пересекают эту плоскость, то линия пересечения параллельна данной прямой
  а а а а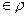 b
b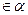 b аIIb
b аIIb
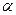
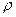
| ||||||
| Две плоскости | ||||||||
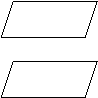 Две плоскости называются параллельными, если они не пересекаются Две плоскости называются параллельными, если они не пересекаются
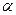
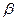
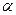 II II 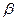
|  Если 2 пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
аIIа1 Если 2 пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны
аIIа1
  а b вIIв1 а b вIIв1
 II II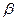
 в в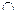 а
а1 b1 в1 а
а1 b1 в1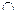 а1
а1в1 а1
а1в1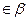
| Если 2 параллельные плоскости пересекаются
  3-й, то прямые пересечения параллельны 3-й, то прямые пересечения параллельны
    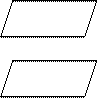 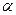 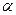 II II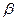 в а II в
в а II в
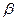 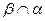
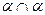 а
а 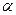 Отрезок параллельных прямых, заключённые между двумя параллельными плоскостями, равны
Отрезок параллельных прямых, заключённые между двумя параллельными плоскостями, равны
а II в | ||||||
Две прямые в простран-
Называются параллель-
ными, если они лежат в одной плоскости и не пересекаются.
 а а 
 в в
| Две прямые
 Через точку вне данной прямой можно провести прямую параллельную этой прямой, и при том только одну. Через точку вне данной прямой можно провести прямую параллельную этой прямой, и при том только одну.
 а в а II в
А а в а II в
А  А А  в в
 Две прямые параллельны 3-й прямой, то они параллельны. Две прямые параллельны 3-й прямой, то они параллельны.
  а а II с
в а а II с
в  а II в
с в II с а II в
с в II с
   Если прямые а и в пересекают другую прямую с в точках А и В под прямым углом, значит они являются параллельными
в с с Если прямые а и в пересекают другую прямую с в точках А и В под прямым углом, значит они являются параллельными
в с с а = В а = В
 А А  В в В в  а =А
а а =А
а  в
а в
а  с
в II c с
в II c
| Если две прямые параллельны и пересечены 3-й прямой, то: 1.
углы равны.
 2. Соответственные углы равны. Односторонние в сумме равны 180 2. Соответственные углы равны. Односторонние в сумме равны 180 . .
 а 7 с
3 1 а 7 с
3 1
 2 4
в 8 5
1=2 4=6
3=4 7=2
5=7 3=8
6=8 1=5 2 4
в 8 5
1=2 4=6
3=4 7=2
5=7 3=8
6=8 1=5
| ||||||
|
|
|
 2014-02-24
2014-02-24 513
513

 А
А


 В1
В1