 Пусть имеется два множества X и Y элементов, вообще говоря, произвольной природы. Пусть задан закон или правило f, по которому элементам множества X ставятся в соответствие элементы множества Y. Тогда говорят, что задана функция или отображение f между множествами X и Y. Если множество X числовое, то говорят о функции числового аргумента. Если множество Y числовое, то говорят о числовой функции.
Пусть имеется два множества X и Y элементов, вообще говоря, произвольной природы. Пусть задан закон или правило f, по которому элементам множества X ставятся в соответствие элементы множества Y. Тогда говорят, что задана функция или отображение f между множествами X и Y. Если множество X числовое, то говорят о функции числового аргумента. Если множество Y числовое, то говорят о числовой функции.
Множество элементов x Î X, которым поставлены в соответствие элементы множества Y называетсяобластью определения отображения f и обозначается D (f); множество элементов у Î Y, которые поставлены в соответствие элементам множества X называетсяобластью значений отображения f и обозначается Е (f);
Физические типы соответствий:
1°. Сюръективное отображение (отображение «на»):

" у Î Y $ x Î X y = f (x);
(не обязательно $!)
2°. Инъективное отображение (вложение):

Е (f) Ì Y, x 1 ¹ x 2 Þ f (x 1) ¹ f (x 2).
3°. Биективное отображение (и сюръективное, и инъективное):

D (f) = X;
Е (f) = Y; x 1 ¹ x 2 Þ f (x 1) ¹ f (x 2).
Def: Множества Х и Y называются равномощными, если существует биективное отображение множества Х на множество Y (взаимнооднозначное соответствие).
Def: Множество равномощное множеству натуральных чисел ℕ называется счетным.
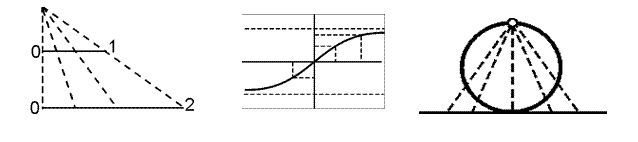
Def: Множество равномощное множеству Х º { x ú x Î(0, 1)} называется множеством мощности континуум.
На рисунках приведены примеры биективных отображений, иллюстрирующих что:
а) множество чисел на интервале (0, 1) и множество чисел на интервале (0, 2) - равно-
мощны.
 б) множество чисел на интервале (0, 1) и множество чисел на вещественной оси – равно-
б) множество чисел на интервале (0, 1) и множество чисел на вещественной оси – равно-
мощны.
в) множество точек на окружности с выколотой точкой и множество чисел на вещественной оси – равномощны.
г) множество ¤ рациональных чисел - счетно.
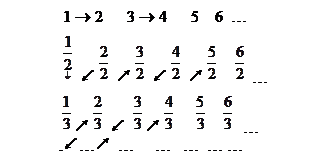
В таблице приведен один из возможных способов нумерации рациональных чисел, что и является доказательством счетности множества ¤ рациональных чисел.
5) Множество вещественных чисел х Î(0, 1) не счетно.
∆ Доказательство проведем от противного. Допустим, что множество вещественных чисел х Î(0, 1) счетно и, следовательно, их можно пронумеровать. Запишем все эти числа в порядке нумерации:
1. 0,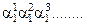 Запишем еще одно число из промежутка (0, 1).
Запишем еще одно число из промежутка (0, 1).
2. 0,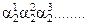 0,
0,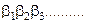
3. 0,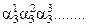 При этом, пусть
При этом, пусть 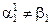 ;
; 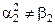 ;
; 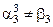 ; …..
; …..
4. ……………… Тогда, совершенно ясно, что это число не совпадает ни
……………… с одним из чисел приведенных в списке, несмотря на то,
что оно принадлежит промежутку (0, 1). Следовательно, по крайней мере одно из чисел промежутка (0, 1), не получило никакого номера. Это противоречит предположению о счетности множества чисел х Î(0, 1). Противоречие и доказывает теорему. ▲
 2014-02-24
2014-02-24 434
434








