2014-02-24
461
.
.
.
Доказательство формул дифференцирования
Таблицу производных надо знать!
Таблицу производных надо знать!
Таблица производных
1°.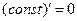 
.
2°.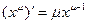 
.
3°.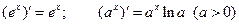 
.
4°.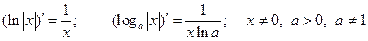 
.
5°. 
.
6°.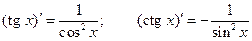 
.
7°. 
.
8°.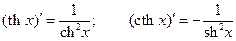 
.
9°.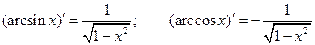 
.
10°.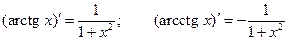 
.
11°.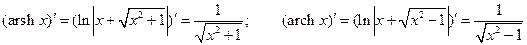 
.
12°.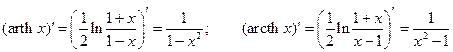 
.
1°.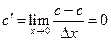 
2°.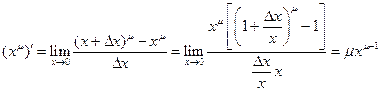 
.
3°.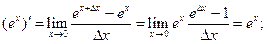 
.
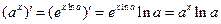4°.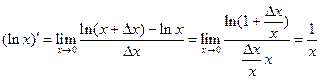 
;
; 
.
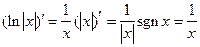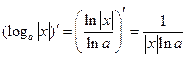5°.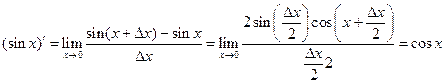 
;
.
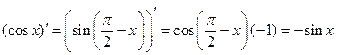6°.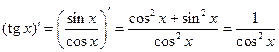 
;
7°.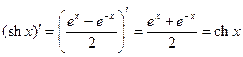 
;
8°.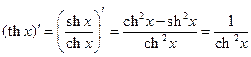 
;
.
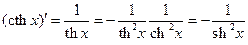9°.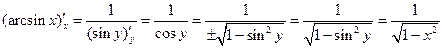 
;
.
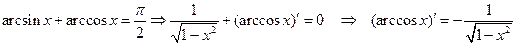10°.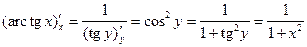 
;
11°.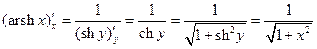 
;
.
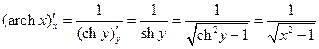12°.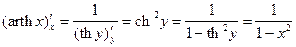 
;
.
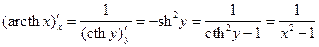13°. Пусть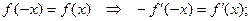 
и пусть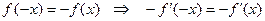 
.
Производная нечетной функции есть функция четная, а производная четной функции – функция нечетная.
14°.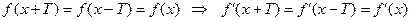 
.
Производная периодической функции есть функция периодическая.
Производная непериодической функции – может быть функцией периодической:
.
Мы дадим индуктивные определения производных и дифференциалов высших порядков:
Def.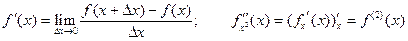 
;
; 
.
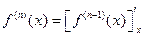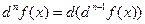Иногда удобно отождествлять саму функцию и производную нулевого порядка.
Когда нам это будет удобно, именно так мы и будем поступать.
