Def. Дифференциалом функции 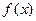 в точке
в точке 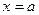 называется главная линейная по приращению аргумента часть приращения функции:
называется главная линейная по приращению аргумента часть приращения функции:
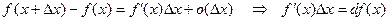 .
.
Записанная формула называется формулой инфинитезимальных (бесконечно малых) приращений.
§. Геометрическая и физическая интерпретация производной и дифференциала
Геометрический смысл производной: Производная функции в точке 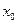 численно равна тангенсу угла наклона касательной к графику функции
численно равна тангенсу угла наклона касательной к графику функции 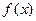 , проведенной через точку графика с абсциссой
, проведенной через точку графика с абсциссой 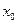 .
.
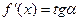 .
.
Физический смысл производной: Производная функции в точке 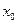 численно равна мгновенной скорости изменения функции при значении аргумента равном
численно равна мгновенной скорости изменения функции при значении аргумента равном 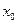 .
.
Геометрический смысл дифференциала: Дифференциал функции в точке 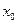 численно равен линейному приращению функции в точке
численно равен линейному приращению функции в точке 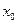 .
.
 2014-02-24
2014-02-24 634
634








