Дифференциалы высших порядков
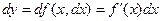 ;
; 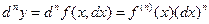 ;
; 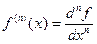 ;
;
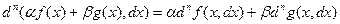 ;
;
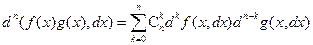 .
.
Последняя из написанных формул это формула Лейбница для высших дифференциалов функций, представленных в виде произведения.
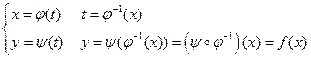 Þ
Þ 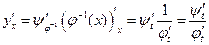 Þ
Þ
Þ 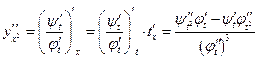 .
.
Если из двух функций заданных и непрерывных на промежутке одна строго монотонна в окрестности точки 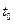 , обе дифференцируемы n -кратно в окрестности этой точки и первая производная строго монотонной функции не равна нулю то в некоторой окрестности
, обе дифференцируемы n -кратно в окрестности этой точки и первая производная строго монотонной функции не равна нулю то в некоторой окрестности 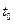 существует функция, заданная параметрически, тоже n -кратно дифференцируемая и ее n -я производная рационально выражается через n первых производных функций
существует функция, заданная параметрически, тоже n -кратно дифференцируемая и ее n -я производная рационально выражается через n первых производных функций  и
и 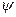 .
.
 2014-02-24
2014-02-24 461
461








