2014-02-24
782
6°..
Производная суммы, произведения и частного дифференцируемых функций
1°.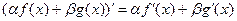 
;
2°.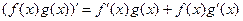 
;
3°.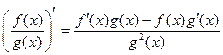 
;
4°.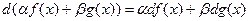 
;
5°.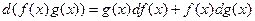 
;
Все эти формулы могут, без большего труда, доказаны.
Пусть заданы функци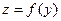и 
и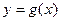 
. Суперпозицией этих двух функций называется функция 
.
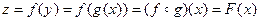Для дифференцирования суперпозиции двух функций запишем
.
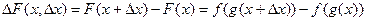
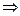
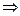
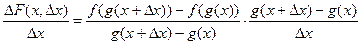Переходя к пределу при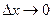 
, получаем: 
.
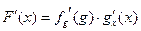Другие формы записи той же формулы:
.
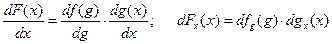Формула эта называется цепным правилом дифференцирования сложной функции.
