Остаточный член в форме Шлёмильха – Роша

Для функции f (x) n раз дифференцируемой на промежутке с концами х и х ₀ и (n +1) раз дифференцируемой внутри него и для любой функции 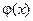заданной на промежутке с концами х и х ₀, дифференцируемой внутри него, имеющей ненулевую производную

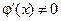() имеет место формула:

.

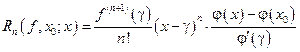В этой формуле g = х ₀ + q (х – х ₀), 0 < q < 1, | x – x ₀| > |g – x ₀| > 0.

D Рассмотрим .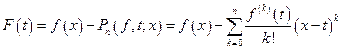

=

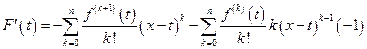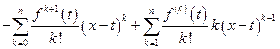= . Во второй сумме положим k = l + 1.

= = .

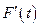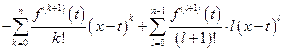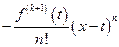Тогда по формуле Коши получаем:

.

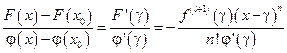Учитывая, что ,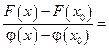

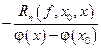получаем: . ▲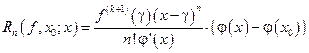

Получен остаточный член в форме Шлёмильха – Роша.