Алгебраическая замкнутость поля комплексных чисел.
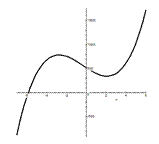
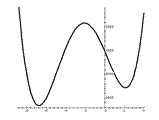
На рисунках слева проиллюстрировано что, полином четной степени может и не иметь вещественных корней, а полином нечетной степени обязательно имеет, по меньшей мере, один вещественный корень. Вопрос: сколько корней, в том числе вещественных, имеет полином произвольной степени?
Т°. (Основная теорема алгебры). Поле комплексных чисел алгебраически замкнуто, т. е. всякий многочлен ненулевой степени с комплексными коэффициентами имеет хотя бы один комплексный корень (в частности это относиться и к многочлену с вещественными коэффициентами).
Если 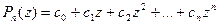 ,
, 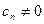 ,
, 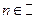 ,
, 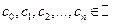
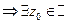
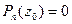 .
.
Теорема была доказана Даламбером (1717 – 1783) и Гауссом (1777 – 1855) еще в XVIII веке, хотя лишь в XIX веке эти доказательства были доведены до полной строгости. В настоящее время существует несколько десятков различных ее доказательств.
∆ Сначала cформулируем очень важный для доказательства
Принцип Руше: Приращение Arg f(z) при движении по замкнутому контуру С в положительном направлении равно 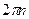 , где n количество нулей функции f (z) внутри области ограниченной контуром С.
, где n количество нулей функции f (z) внутри области ограниченной контуром С.
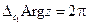 (для контура С 1 содержащем внутри себя начало координат);
(для контура С 1 содержащем внутри себя начало координат);
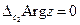 (для контура С 2 не содержащем внутри себя начало координат).
(для контура С 2 не содержащем внутри себя начало координат).
Теперь рассмотрим 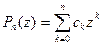 ,
, 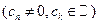 и преобразуем его к виду
и преобразуем его к виду
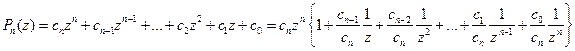 .
.
Выберем замкнутый контур C так:
C – окружность, с центром в начале координат пробегаемая против часовой стрелки. Радиус окружности R выберем так, чтобы 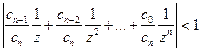 .
.
Это всегда можно сделать с помощью выбора достаточно большого R ибо
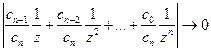 при
при 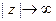
Тогда: 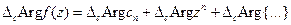 .
.
При этом 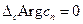 т.к. константа и ее аргумент не изменяются при обходе контура,
т.к. константа и ее аргумент не изменяются при обходе контура, 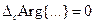 т.к. выражение
т.к. выражение 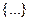 при обходе контура С, описывает контур не содержащий начало координат и, следовательно:
при обходе контура С, описывает контур не содержащий начало координат и, следовательно:
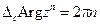 т.е.
т.е. 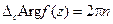 .
.
и, согласно принципу Руше, функция 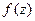 имеет внутри контура (т.е. на комплексной плоскости) n корней, возможно совпадающих.
имеет внутри контура (т.е. на комплексной плоскости) n корней, возможно совпадающих.
 2014-02-24
2014-02-24 1510
1510








