1°. 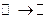 ,
, 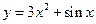 . Вещественно значная функция вещественного аргумента.
. Вещественно значная функция вещественного аргумента.
2°. 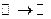 ,
, 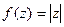 . Вещественно значная функция комплексного аргумента.
. Вещественно значная функция комплексного аргумента.
3°. 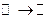 ,
, 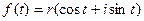 :
: 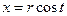 ,
, 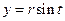 ,
, 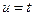 . Комплексно значная функция вещественного аргумента.
. Комплексно значная функция вещественного аргумента.
4°. 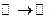 ,
, 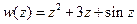 . Комплексно значная функция комплексного аргумента.
. Комплексно значная функция комплексного аргумента.
5°. Комплексно значная функция натурального аргумента называется комплексно значной последовательностью 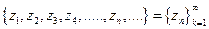 .
.
§ Предел. Дифференцируемость. Непрерывность. Интегрируемость.
Комплексно значная функция комплексно значного аргумента – векторно значная функция векторного аргумента.
Def. Точка 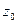 называется точкой сгущения множества М (предельной точкой), если
называется точкой сгущения множества М (предельной точкой), если 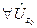 существует, по крайней мере одна, (а значит бесконечно много) отличная от
существует, по крайней мере одна, (а значит бесконечно много) отличная от 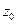 точка из множества M.
точка из множества M.
Def. 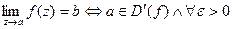
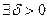
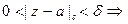
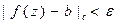 .
.
(a, b, z 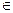 C).
C).
*. Если комплексно значная функция имеет предел, то её модуль также имеет предел и при этом: 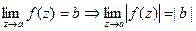 .
.
Δ Факт этот следует из неравенства: 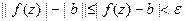
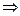
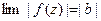 . ▲.
. ▲.
Если 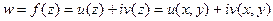 , при
, при 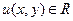 ,
, 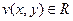 то
то
*) 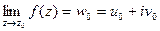

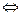
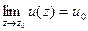
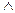
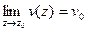 ;
;
*) 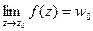 ,
, 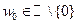
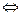
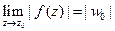
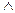
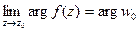
*) 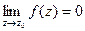
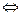
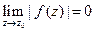 .
.
Непрерывность в терминах пределов и неравенств формулируется так же, как и для вещественно значных функций.
Производная и дифференциал функции определяется в полной аналогии с определениями для функций вещественного аргумента. И результаты зачастую очень похожи. Однако …
Для комплексно-значных функций требования дифференцируемости накладывает существенные ограничения.
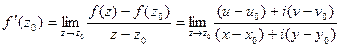 .
.
Переходя в полученном выражении к пределу, получаем:
1) 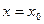 ,
, 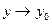 ,
, 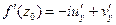 ; 2)
; 2) 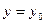 ,
, 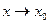 ,
, 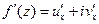 .
.
Из двух различных записей для 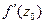 делаем вывод: функция комплексного аргумента
делаем вывод: функция комплексного аргумента 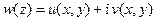 дифференцируема тогда и только тогда, когда выполняются условия:
дифференцируема тогда и только тогда, когда выполняются условия: 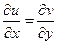 ;
; 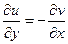 . Эти условия называются условиями Коши – Римана.
. Эти условия называются условиями Коши – Римана.
При этом из условий Коши – Римана для дифференцируемой функции следует:
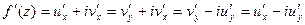 ;
;
Кроме того непосредственными вычислениями удается установить, что:
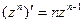 ;
; 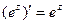 ;
; 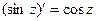 ; ……
; ……
 2014-02-24
2014-02-24 1102
1102
