Комплексные корни многочлена с вещественными коэффициентами

Рассмотрим 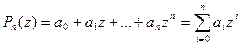, (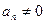и 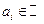) и пусть 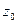является корнем 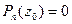многочлена. Тогда:

.

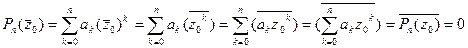Т.е. если число 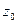является корнем уравнения n -й степени с вещественными коэффи- циентами, то 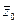также является корнем того же многочлена.

Следствие: Уравнение нечетной степени с вещественным коэффициентом имеет хотя бы

один вещественный корень.

Следствие: Уравнение четной степени с вещественным коэффициентом может и не иметь

вещественных корней.

При этом: =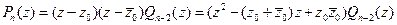

= = .

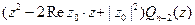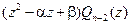Итог:

Если 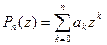многочлен с вещественными коэффицциентами (, )

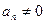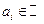То: 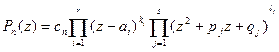причем , , .

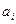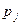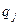
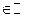
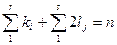Разложение многочлена на линейные и квадратичные множители с вещественными коэффициентами (причем квадратичные множители не имеют вещественных корней) называется разложением многочлена на неприводимые множители.