Дополнение 4
Т.
- Пусть Х - некоторое числовое поле. Если $ М Î R ô" х Î Х М ³ х то множество Х называется ограниченным сверху, а число М называется его верхней границей. Наименьшая из верхних границ М * множества Х называется его верхней гранью и обозначается М * = sup Х. Таким образом, число М Î R называются верхней гранью множества Х, если:
а) " х Î Х х ≤ М *; б) "e>0 $ х 1Î Х ê х 1 > М * – e.
Если М *Î Х, то оно называется наибольшим элементом множества Х и обозначается
ô" х Î Х * = sup Х.
- Пусть Х – некоторое числовое множество. Если $ m Î R ô" х Î Хх ≤ m то множество Х называется ограниченным снизу, а число m называется его нижней границей. Наибольшая из нижних границ m * множества Х называется его нижней гранью и обозначается m * = inf Х. Таким образом, число m Î R называется нижней гранью множества Х, если:
а) " х ≤ Х х ≥ m *; б) "e > 0 $ х 2Î Х ï х 2 < m * + e.
Если m *Î Х то оно называется наименьшим элементом множества Х и обозначается
m * = min Х.
- Множество Х ограниченное сверху и ограниченное снизу называется ограниченным.
- Понятие ограниченности, верхней и нижней границ и граней, а также наибольшего и наименьшего значения функции y = y (x) определяются как соответствующие элементы ее области значений Е (y).
- Понятие предела функции.
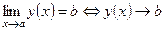 при
при 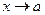
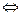 а Î D (y)¢
а Î D (y)¢  " х Î D (y) "e>0 $d(e)>0 ê х Î
" х Î D (y) "e>0 $d(e)>0 ê х Î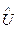 a ,δ Þ y Î Ub ,ε.
a ,δ Þ y Î Ub ,ε.
Здесь D (y) – область определения функции y (x), D (y)¢ – множество ее предельных точек,
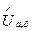 – проколотая d-окрестность точки, Ub ,e – e-окрестность точки b. В частности,
– проколотая d-окрестность точки, Ub ,e – e-окрестность точки b. В частности,
если в качестве окрестности точки х 0Î R взять равносторонний интервал с центром в
х 0, то: 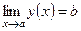 Û
Û 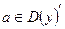
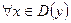
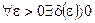 ê
ê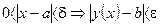 .
.
- Формулы связанные с замечательными пределами (везде х®0)
I. Замечательные II. Замечательные III. Замечательные
пределы эквивалентности равенства
1. 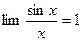 1.
1. 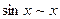 1.
1. 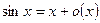
2. 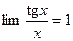 2.
2. 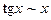 2.
2. 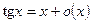
3. 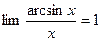 3.
3.  3.
3. 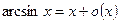
4. 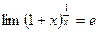 4.
4. 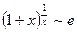 4.
4. 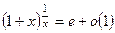
5. 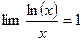 5.
5. 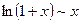 5.
5. 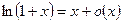
6. 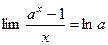 6.
6. 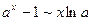 6.
6. 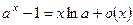
7. 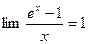 7.
7. 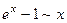 7.
7. 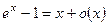
8. 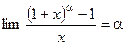 8.
8.  8.
8. 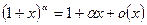
IV. Пять замечательных разложений в ряд.
1. 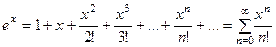
2. 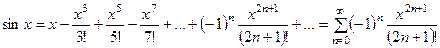
3. 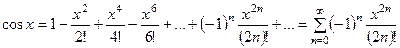
4. 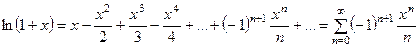
5. 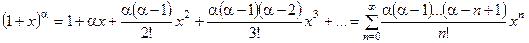
А. З.
1(389). Определить нижнюю и верхнюю грань функции 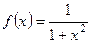 , для х Î R.
, для х Î R.
2(401 * ). На языке «e- d» доказать, что 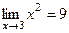 . Указать правило нахождения «d» по заданно-
. Указать правило нахождения «d» по заданно-
му «e».
3. Во всех нижеследующих записях предполагается, что a Î D (f)¢ и x Î D (f). Для каких функций f (x) справедливы утверждения:
а) "e > 0 $ d > 0 | 0 < | х – а |< d Þ | f (x) – b | < e;
б) $ e > 0 $ d > 0 | 0 < | х – а | < d Þ | f (x) – b | < e;
в) "e $ d > 0 | 0< | х – а | < d Þ | f (x) – b | < e;
г) "e > 0 "d > 0 | 0 < | х – а | < d Þ | f (x) – b | < e;
д) "e > 0 $ d | 0 < | х – а | < d Þ | f (x) – b | < e;
е) "e > 0 $ d > 0 | | х – а | < d Þ | f (x) – b | < e;
ж) "e > 0 $ d > 0 | | х – а | > d Þ | f (x) – b | < e;
з) "e > 0 $ d > 0 | 0 < | х – а | < d Þ | f (x) – b | > e;
и) "e>0 $d>0 | 0<|х–а|<d Þ f(x)–b>e
к) "e>0 $d>0 | 0<|х–а|<d Þ f(x)>e
4(407 * ). Пусть y = f (x). Сформулировать на языке ”e – d” следующие утверждения:
а) y ® b – 0 при х ® а; б) y ® b – 0 при х ® а + 0;
в) y ® b + 0 при х ® а – 0; г) y ® b + 0 при х ® + ¥;
д) y ® b при х ® – ¥; е) y ® b – 0 при х ® + ¥;
ж) y ® ¥ при х ® – ¥; з) y ® – ¥ при х ® + ¥.
Найти пределы:
5(418*) 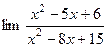 а) х ® 1, б) х ® 2, в) х ® 5, г) х ® 3.
а) х ® 1, б) х ® 2, в) х ® 5, г) х ® 3.
6(419) 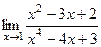 . 7(420)
. 7(420) 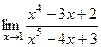 . 8(425*)
. 8(425*) 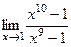 . 9(436)
. 9(436) 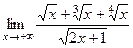 . 10(446)
. 10(446) 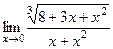 . 11(447)
. 11(447) 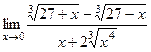 .
.
12(448) 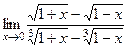 . 13(457)
. 13(457) 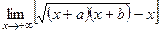 . 14(458)
. 14(458) 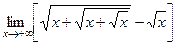 . 15(462)
. 15(462) 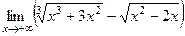 . 16(503)
. 16(503) 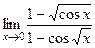 . 17(505)
. 17(505) 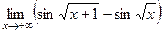 .
.
18(507)  . 19(508)
. 19(508) 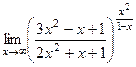 . 20(509)
. 20(509) 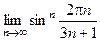 .
.
21(517) 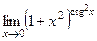 . 22(519)
. 22(519) 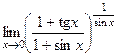 . 23(531)
. 23(531) 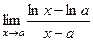 (а > 0).
(а > 0).
24(532) 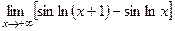 . 25(533)
. 25(533) 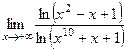 .
.
26(561) 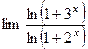 а) х ® – ¥, б) х ® + ¥. 27(562)
а) х ® – ¥, б) х ® + ¥. 27(562) 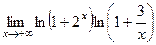 .
.
28(563) 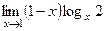 . 29(1324)
. 29(1324)  . 30(1325)
. 30(1325)  .
.
31(1349) 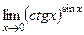 . 32(1398)
. 32(1398) 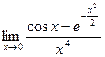 . 33(1399)
. 33(1399) 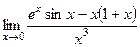 . 34(1400)
. 34(1400) 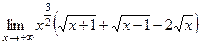 . 35(1401)
. 35(1401) 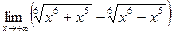 .
.
36(1402) 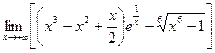 . 37(1406.1)
. 37(1406.1) 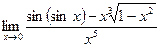 .
.
 2014-02-24
2014-02-24 361
361







