Отсюда находим цену игры и вероятности применения стратегий
Пример
Проверим наличие седловой точки.
Для игрока А: Max (1, 1, 3) = 3
Для игрока В: min(7, 4, 5, 7) = 4
Так как значения не совпадаю, Седловой точки нет, а цена игры V находится в промежутке [3; 4].
Решим задачу в смешанных стратегиях. Для этого составим пару двойственных задач.
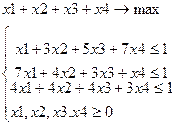
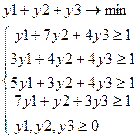
Решая задачи, находим, что
X={0.05, 0.15, 0, 0.07}
Y={0.07, 0.05, 0.15}
F=0.27
V=1/0.27=3.7
P={0.19, 0.56, 0.26}
Q={0.26, 0.19, 0.56}
При поиске оптимальных стратегий в матричных играх размерностей 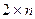 и
и 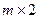 целесообразно использовать графический метод решения задач линейного программирования и свойства оптимальных планов пары двойственных задач: если в оптимальном плане задачи переменная положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в равенство; если оптимальным планом задачи ограничение обращается в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю.
целесообразно использовать графический метод решения задач линейного программирования и свойства оптимальных планов пары двойственных задач: если в оптимальном плане задачи переменная положительна, то соответствующее ограничение двойственной задачи ее оптимальным планом обращается в равенство; если оптимальным планом задачи ограничение обращается в строгое неравенство, то в оптимальном плане двойственной задачи соответствующая переменная равна нулю.
Пример. Решить игру с платежной матрицей
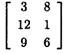
графическим методом.
Решение. В данном случае 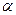 = 6,
= 6, 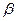 = 8, т.е.
= 8, т.е. 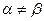 , а поэтому для определения оптимальных смешанных стратегий игроков составляем задачи
, а поэтому для определения оптимальных смешанных стратегий игроков составляем задачи
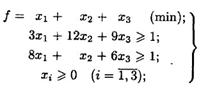
(1)
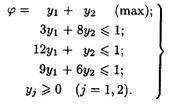
(2)
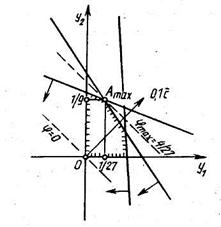
Поскольку одна из задач содержит две переменные, то, решим ее графически, находим: 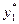 =1/27,
=1/27, 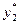 =1/9,
=1/9, 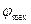 =4/27. Используя формулы
=4/27. Используя формулы 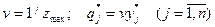 , получаем:
, получаем: 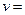 27/4,
27/4, 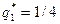 ,
, 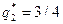 .
.
Для определения оптимальной смешанной стратегии 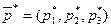 найдем сначала решение двойственной задачи. В оптимальном плане задачи (2)
найдем сначала решение двойственной задачи. В оптимальном плане задачи (2) 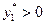 и
и 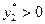 , поэтому оба ограничения двойственной задачи (1) ее оптимальным планом
, поэтому оба ограничения двойственной задачи (1) ее оптимальным планом 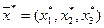 обращаются в равенства. Кроме того, значениями
обращаются в равенства. Кроме того, значениями 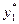 и
и 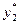 второе ограничение задачи (2) обращается в строгое неравенство. Следовательно, в оптимальном плане задачи (1) соответствующая ему вторая переменная равна нулю, т. е.
второе ограничение задачи (2) обращается в строгое неравенство. Следовательно, в оптимальном плане задачи (1) соответствующая ему вторая переменная равна нулю, т. е. 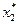 =0. Учитывая сказанное, для определения
=0. Учитывая сказанное, для определения 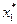 и
и  получаем уравнения
получаем уравнения 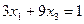 и
и 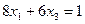 , совместное решение которых дает
, совместное решение которых дает 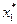 = 3/54,
= 3/54,  = 5/54. Используя формулы
= 5/54. Используя формулы 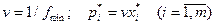 , определяем
, определяем 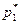 =3/8,
=3/8, 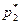 =0,
=0, 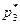 =5/8. Итак, решение игры найдено:
=5/8. Итак, решение игры найдено:
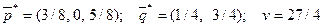 .
.
 2014-02-24
2014-02-24 1737
1737
